Алгоритм построения сокращенной ДНФ с помощью КНФ
(метод Нельсона) Пусть f (x 1, …, xn) есть некоторая функция алгебры логики. Построим для f некоторую КНФ. Осуществим далее следующие преобразования. 1. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание. В результате получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ. 2. В полученном выражении удалим нулевые дизъюнктивные слагаемые. 3. В полученном выражении проведем все поглощения, а затем удалим дублирующие члены. В результате проведенных операций получим сокращенную ДНФ функции f. Покажем это. Для каждой элементарной дизъюнкции D в КНФ и каждой элементарной конъюнкции K в сокращенной ДНФ (сокр. ДНФ) существует некоторый множитель вида x из K, содержащийся в D, т.е.
Допустим противное: в КНФ существует элементарная конъюнкция D, в сокращенной ДНФ существует элементарная конъюнкция K, для которой всякий множитель вида xa из K не входит в D. Не уменьшая общности возьмем для простоты
Положим x 1 = a 1, …, xk = ak, xk +1 = ck +1 ¹ ak +1, …, xr = cr ¹ ar. Тогда K(a 1, …, ak) = 1, и потому f (a 1, …, ak, ck +1, …, cr) = 1. С другой стороны, D (ck +1, …, cr) = 0, и потому f (a 1, …, ak, ck +1, …, cr) = 0. Противоречие. Пусть по-прежнему для простоты произвольный простой импликант K из сокращенной ДНФ равен Так как Пример 3. Построим сокращенную ДНФ этим способом для функции f = (1111010010101111) из примера 1:
Сокращенная ДНФ для функции
что, естественно, совпадает с результатом примера 1. Пример 4. Построить сокращенную ДНФ по заданной КНФ После раскрытия скобок имеем: После второго этапа получаем сокращенную ДНФ: Тупиковой ДНФ (ТДНФ) функции f называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции f. Теорема. Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ. Доказательство. В МДНФ входят только простые импликанты, иначе некоторые множители в непростом имликанте можно удалить в противоречие с минимальностью исходной ДНФ. В МДНФ нет лишних импликант, иначе исходная ДНФ не является минимальной. Вывод. Для получения МДНФ функции f необходимо построить все ТДНФ функции f и выбрать из них те, которые содержат минимальное число букв.
|

 " D Î ДНФ " K Î сокр. ДНФ $ xa Î K (xa Î D).
" D Î ДНФ " K Î сокр. ДНФ $ xa Î K (xa Î D).

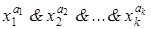 . Тогда элементы
. Тогда элементы 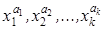 попадут в не менее чем k скобок из КНФ. Если допустим, что этого нет, то при перемножении скобок из КНФ не получим дизъюнктивного слагаемого, которое содержало бы множители
попадут в не менее чем k скобок из КНФ. Если допустим, что этого нет, то при перемножении скобок из КНФ не получим дизъюнктивного слагаемого, которое содержало бы множители 







