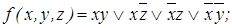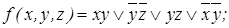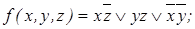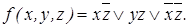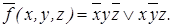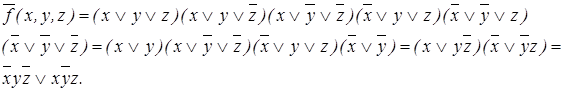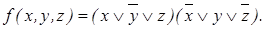Алгоритм минимизации функций в классе нормальных форм
Пусть f – функция алгебры логики. 1. Строим все МДНФ функции f. 2. Строим все МКНФ функции f. 3. Из построенных минимальных форм выбираем простейшие (по числу букв). Пример 6. В классе нормальных форм минимизировать функцию f =(01011110). 1. Строим СДНФ для функции f:
2. Строим сокращенную ДНФ функции f:
3. Строим матрицу покрытий (таблица 3.6). Таблица 3.6
Решеточное выражение E = (1 Ú 2) 1 (3 Ú 4) 4 = 134 Ú 124. 4. Строим все тупиковые ДНФ функции f:
5. Обе построенные ТДНФ являются минимальными. 6. Повторяем эти этапы для функции ` f. СДНФ: Сокращенная ДНФ: Строим матрицу покрытий (таблица 3.7). Таблица 3.7
Решеточный многочлен E = 112 = 12. Единственная тупиковая ДНФ (она же минимальная) для функции Пример 7. В классе нормальных форм минимизировать функцию f =(11011011). 1. СДНФ: 2. Сокращенная ДНФ:
3. Строим матрицу покрытий (таблица 3.8).
Таблица 3.8
E = (3 Ú 6) (4 Ú 6) (4 Ú 5) (2 Ú 3) (1 Ú 2) (1 Ú 5) = 1246 Ú 1356 Ú 134 Ú 256 Ú 2345. 4. Тупиковые ДНФ функции f:
5. Минимальные ДНФ функции f:
6. Повторяем указанные выше этапы для функции ` f. СДНФ: Сокращенная ДНФ:
Построенная сокращенная ДНФ функции ` f является для нее тупиковой и минимальной. Минимальная КНФ функции Построенные МДНФ и МКНФ имеют одно и то же число букв; все они составляют минимальные формы для f:
|
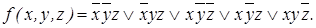
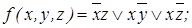
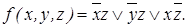
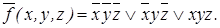
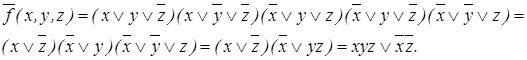
Минимальная КНФ функции 
Из построенных МДНФ и МКНФ выбираем простейшую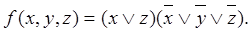 
=
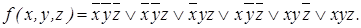
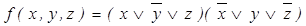