Первое начало термодинамики
Первое начало термодинамики представляет собой одну из формулировок закона сохранения энергии. Для закрытой системы первое начало может быть сформулировано следующим образом: В любом процессе изменение внутренней энергии равно разности между количеством подведенной теплоты и количеством совершенной работы:
или для бесконечно малого изменения внутренней энергии
Теплота и работа являются функциями процесса, их изменение зависит от пути протекания процесса. Поэтому бесконечно малые величины теплоты и работы не обладают свойствами дифференциала и для их обозначения используют греческую букву δ. Внутренняя энергия, напротив, является функцией состояния, поэтому для обозначения её бесконечно малого изменения используется знак дифференциала (dU). В химической термодинамике рассматриваются процессы, связанные с превращениями теплоты и работы, поэтому первое начало термодинамики представляют в виде
для бесконечно малого процесса или для конечного процесса:
Итак, согласно первому началу термодинамики: Теплота, подведенная к закрытой системе, расходуется на увеличение ее внутренней энергии и совершение работы. В химико-технологических системах обычно совершается работа против внешнего давления. В термодинамике используют следующую систему знаков. Положительной считают теплоту, подведенную к системе, а отрицательной – отведенную от нее. Работу, совершенную системой, считают положительной, а совершаемую над системой, например, работу сжатия – отрицательной.
2. 2. 1. Работа расширения идеального газа Рассмотрим работу расширения газов, которое происходит во многих химико-технологических процессах. При не очень высоких давлениях (P < 50 ат) свойства газов близки к свойствам идеального газа. В общем случае работа расширении газа в бесконечно малом процессе равна
Для реального конечного процесса расширения газа
При не очень высоких давлениях (P < 50 ат) свойства газов близки к свойствам идеального газа. Поэтому для вычисления работы расширения будем использовать уравнение состояния идеального газа Менделеева-Клапейрона. Работа расширения как функция процесса зависит от условий, в которых протекает процесс. Изохорный процесс (V = const): Если процесс протекает при постоянном объеме системы, то изменение объема dV = 0, тогда
Изотермический процесс (T = const): Из уравнения Менделеева-Клапейрона
тогда при T = const
Изобарный процесс (P = const):
Изобарно-изотермический процесс (P = const и T = const): Из уравнения Менделеева-Клапейрона
Таким образом, в изобарно-изотермических условиях работа расширения может совершаться только за счет изменения числа молей газа. 2. 2. 2. Теплота процесса в различных условиях Изохорный процесс (V = const): Работа изохорного процесса W = 0. Тогда, как следует из первого начала термодинамики, теплота процесса в изохорных условиях QV равна изменению внутренней энергии:
Так как внутренняя энергия является функцией состояния, то в изохорных условиях теплота Изотермический процесс (T = const): По закону Гей-Люсака-Джоуля внутренняя энергия идеального газа зависит только от температуры и не зависит от объема и давления. Следовательно, в изотермическом процессе не происходит изменения внутренней энергии (Δ U = 0). Тогда из первого начала термодинамики следует
Таким образом, вся теплота в изотермическом процессе идет на совершение работы, Работа изотермического процесса совершается за счет подведенной теплоты. Изобарный процесс (P = const):
или для конечного процесса
Функция H = U + PV называется энтальпией. Энтальпия, как и внутренняя энергия, является функцией состояния, поэтому в изобарных условиях теплота QP приобретает свойства функции состояния. Изохорный и изобарный тепловые эффекты связаны соотношением
Все выведенные закономерности для расчета теплоты процесса выполняются и для химических реакций. Если в результате химической реакции теплота поглощается, то тепловой эффект считается положительным (Q > 0), а реакция называется эндотермической. Если в результате химической реакции теплота выделяется, то тепловой эффект считается отрицательным(Q < 0), а реакция называется экзотермической. Теплота, которая выделяется или поглощается в результате химической реакции, зависит от условий проведения реакции. При проектировании химико-технологических систем очень важно знать величину и знак теплового эффекта реакции. В химико-технологических системах реакции проводят чаще всего в изобарно изотермических условиях. Методы расчета и измерения тепловых эффектов химических реакций рассматриваются в разделе физической химии – термохимии. Рассмотрим практически важные из них. 2. 2. 3. Закон Гесса. Расчет тепловых эффектов химических реакций с использованием стандартных теплот образования и сгорания. Закон Гесса является основным законом термохимии. Он гласит: Тепловой эффект процесса не зависит от пути его протекания (промежуточных стадий), а определяется начальным и конечным состоянием системы при условии, что давление и температура или объем системы и температура в ходе всего процесса остаются постоянными. Закон Гесса позволяет рассчитывать тепловые эффекты реакций, если известны тепловые эффекты других реакций с участием тех же веществ. Из закона Гесса следует два важных следствия. 1. Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ (с учетом стехиометрических коэффициентов). Теплотой образования веществаназывается тепловой эффект реакции образования одного моля вещества из простых веществ. Простым веществом называется химическое соединение, состоящее из атомов одного элемента, в наиболее устойчивой модификации при данных условиях. В изобарных условиях теплота образования обозначается Δ Hf (f – сокращение от английского слова formation). Значения теплот образования при стандартных условиях Тепловой эффект реакции в изобарных условиях Δ rH можно рассчитать, в соответствии со следствием из закона Гесса, по уравнению:
где индексы i относятся к исходным веществам или реагентам (исх.), а индексы j – к конечным веществам или продуктам реакции (кон.); В стандартных условиях тепловой эффект химической реакции
2. Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции (с учетом стехиометрических коэффициентов). Теплотой сгорания вещества Δ Hc (combustion – горение)называется тепловой эффект реакции сгорания одного моля вещества в избытке кислорода до CO2, H2O(ж.), N2, SO2 и галогеноводородов. Стандартные теплоты сгорания Тепловой эффект химической реакции с использованием теплот сгорания можно рассчитать по уравнению
2. 2. 4. Зависимость тепловых эффектов химических реакций от температуры. Закон Кирхгофа Пользуясь следствиями из закона Гесса можно рассчитать тепловой эффект реакции только при стандартной температуре 298 К, так как в справочниках приводятся только стандартные теплоты образовании и сгорания. Большинство же химических реакций в химико -технологических системах ведут при повышенных температурах, чтобы повысить скорость реакций и, следовательно, повысить производительность системы. Для того, чтобы рассчитать тепловой эффект химической реакции при любой температуре надо знать вид зависимости теплового эффекта от температуры Δ rH = f (T). Рассмотрим реакцию
протекающую в изобарных условиях. Тепловой эффект реакции QP = Δ rH можно представить как разность сумм энтальпий продуктов реакции и исходных веществ:
Продифференцируем полученное выражение по температуре:
Производная энтальпии по температуре
Тогда
или в общем виде
где Δ CP – характеризует изменение изобарной теплоемкости системы в результате протекания химической реакции и называется температурным коэффициентом теплового эффекта реакции. Полученное выражение
называется дифференциальным уравнением Кирхгофа. Из него следует, что зависимость теплового эффекта от температуры определяется знаком Δ rCP, т.е. зависит от того, что больше, суммарная теплоемкость исходных веществ или суммарная теплоемкость продуктов реакции. Проанализируем дифференциальное уравнение Кирхгофа. 1. Если температурный коэффициент Δ rCP > 0, то производная 2. Если температурный коэффициент Δ rCP < 0, то производная 3. Если температурный коэффициент Δ rCP = 0, то производная Дифференциальные уравнения удобны для анализа, но неудобны для расчетов. Чтобы получить уравнение для расчета теплового эффекта химической реакции, проинтегрируем дифференциальное уравнение Кирхгофа, разделив переменные:
Теплоемкости веществ зависят от температуры, следовательно, и
Тогда
откуда
При стандартном давлении
Полученное уравнение называется интегральным уравнением Кирхгофа. Оно позволяет рассчитать изобарный тепловой эффект химической реакции при любой температуре, если известен ее тепловой эффект при стандартной температуре (T = 298 К).
|
,
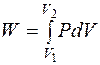
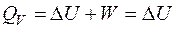
приобретает свойства функции состояния.
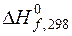для большого количества веществ приведены в справочниках.
,
и 
- стехиометрические коэффициенты в уравнении реакции для исходных веществ и продуктов реакции, соответственно.
может быть рассчитан по справочным значениям теплот образования 
можно найти в справочниках, однако, они приведены для значительно меньшего количества веществ (в основном органических), чем теплоты образования.
,
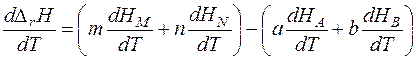
для вещества является его истинной изобарной теплоемкостью, так как она характеризует бесконечно малое количество теплоты, необходимое для нагревания вещества на бесконечно малую температуру в изобарных условиях:
> 0 и функция 
возрастающая. Следовательно, тепловой эффект реакции с ростом температуры увеличивается.
. Следовательно, тепловой эффект реакции не зависит от температуры. Этот случай на практике не встречается.
. Однако, в области обычно используемых в химико-технологических процессах температурах эта зависимость не значительна. Для практических целей пользуются средними теплоемкостями веществ в интервале температур от 298 К до заданной температуры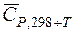 
, которые приводятся в справочниках. Температурный коэффициент теплового эффекта, рассчитанный с использованием средних теплоемкостей:
,
