Константы равновесия
В разд. 2. 3. 3. 2 было показано, что при химическом равновесии свободная энергия Гиббса принимает минимальное значение, и далее ее изменения не происходит: Δ rG = 0. Уравнение изотермы химической реакции при равновесии примет вид:
Обозначим
тогда
или
Полученное уравнение называется частным уравнением изотермы химической реакции. Оно справедливо для состояния равновесия, а выражение Термодинамическая константа равновесия может быть рассчитана, если известно изменение энергии Гиббса системы в результате протекания химической реакции при стандартном давлении и данной температуре:
Термодинамическая константа равновесия зависит от природы реагирующих веществ и температуры, но не зависит от давления, поскольку изменение стандартной энергии Гиббса не зависит от давления по определению. Поскольку
Термодинамическая константа равновесия может быть выражена как через активности веществ, участвующих в реакции, Ka (п. 3. 1.), так и через фугитивности Kf:
Термодинамические константы равновесия являются безразмерными величинами. Кроме термодинамических констант равновесие могут характеризовать практические константы равновесия. Практические константы равновесия могут быть рассчитаны, если при равновесии определить количества или концентрации веществ, участвующих в реакции тем или иным методом химического или физико-химического анализа. Они могут быть выражены · через числа молей веществ ni, j в равновесии:
· через молярные концентрации веществ Ci, j в равновесии:
· через мольные доли веществ Ni, j в равновесии:
· через парциальные давления веществ Pi, j в равновесии:
В отличие от термодинамических констант равновесия, практические константы являются размерными величинами. Между термодинамическими и практическими константами равновесия существует определенная математическая связь. Найдем связь между термодинамической константой равновесия Ka и константой равновесия, выраженной через приведенные парциальные давления. Так как
где При давлениях ≤ 50 атмосфер свойства газов близки к свойствам идеальных газов, и γ i, j = 1. Тогда K γ = 1 и
Таким образом, если химическая реакция протекает при не очень высоких давлениях (P ≤ 50), то константа равновесия, выраженная через приведенные давления, равна термодинамической константе равновесия и является безразмерной величиной. Найдем связь между константой равновесия, выраженной через приведенные давления
а мольные доли выражаются как отношения
то
При подстановке последнего выражения в формулу константы равновесия, выраженной через приведенные давления, получим
где Связь термодинамической Ka =
|


 ,
,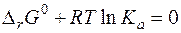


 величина константы равновесия может принимать значения от нуля до бесконечности
величина константы равновесия может принимать значения от нуля до бесконечности
 ,
, ;
; ;
; ;
;
 ,
, ,
,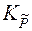 - константа равновесия, выраженная через приведенные парциальные давления
- константа равновесия, выраженная через приведенные парциальные давления  .
. ,
, ,
,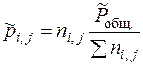
 ,
, .
.


