Второе начало термодинамики. Одной из важнейших задач химической термодинамики является выяснение принципиальной возможности (или невозможности) самопроизвольного протекания химической
Одной из важнейших задач химической термодинамики является выяснение принципиальной возможности (или невозможности) самопроизвольного протекания химической реакции в рассматриваемом направлении. В тех случаях, когда становится ясно, что данное химическое взаимодействие происходить может, необходимо определить степень превращения исходных веществ и выход продуктов реакции, то есть полноту протекания реакции. Предложены два метода определения возможности и направления протекания самопроизвольных процессов: метод факторов интенсивности и метод термодинамических функций. - Метод факторов интенсивности. Интенсивными называются те свойства системы, которые не зависят от массы или количества вещества: температура, давление, концентрации и др. Согласно этому методу, самопроизвольно процессы могут протекать в направлении выравнивания факторов интенсивности (охлаждение - выравнивание температуры, диффузия газов - выравнивание давления или концентрации). Равновесию соответствует состояние, в котором значения фактора интенсивности одинаковы для всех частей системы. Однако данный метод имеет ограничения, он неприменим к однородным системам. - Метод термодинамических функций. В соответствии с этим методом, самопроизвольно может протекать лишь тот процесс, в ходе которого определенная термодинамическая функция достигает своего экстремального значения (минимума или максимума). Причем экстремум характерен для состояния равновесия системы. Для каждого конкретного случая подбирается своя функция, которая в ходе самопроизвольного процесса либо растет, либо уменьшается, достигая своего экстремального значения к моменту достижения системой состояния равновесия. Этот метод является более общим подходом. Термохимические исследования показывают, что большинство химических реакций сопровождается экзотермическим эффектом. Так, например, стандартная теплота образования более чем 90 % неорганических соединений имеет отрицательное значение (Δ Hf < 0). Следовательно, большая часть химических соединений обладает меньшей энергией, чем суммарный запас энергии простых веществ, из которых получены сложные вещества. Основываясь на этом наблюдении, предположили, что реакция идет в том направлении, которое сопровождается выделением теплоты (принцип Бертло-Томсена).Однако существование эндотермических реакций говорит о том, что величина теплового эффекта не может служить универсальным критерием для выбора направления самопроизвольного процесса. Более того, в рамках первого начала термодинамики дать ответы на все эти вопросы не представляется возможным. Направление протекания самопроизвольного процесса можно определить на основе второго закона или начала термодинамики, сформулированного, например, в виде постулата Клаузиуса: Теплота сама собой не может переходить от холодного тела к горячему, т. е. невозможен такой процесс единственным результатом которого был бы переход теплоты от тела с более низкой температурой к телу с более высокой температурой. Предложено множество формулировок второго начала термодинамики. Формулировка Томсона - Планка: Невозможен вечный двигатель второго рода, т. е. невозможна, такая периодически действующая машина, которая бы позволяла получать работу только за счет охлаждения источника тепла. 2. 3. 1. Термодинамически обратимые и необратимые процессы. В термодинамике используется понятие обратимых (или квазистатических) процессов. Термодинамическое понятие обратимого процесса не связано с направлением процесса (реакции), оно лишь указывает на определенный способ проведение процесса (реакции). Обратимым называется процесс, который осуществляется таким образом, что имеется возможность возвращения системы в исходное состояние через те же самые промежуточные квазиравновесные состояния, которые он проходил в прямом направлении, и при этом ни в самой системе, ни в окружающей среде не остается никаких стойких изменений. В необратимом процессе нет возможности возвращения системы в исходное состояние через те же самые промежуточные состояния. Термодинамически обратимыми можно, например, считать процессы: · сжатия (расширения) идеального газа, когда внешнее давление лишь на бесконечно малую величину отличается от давления газа; · нагревания или охлаждения системы, если температура источника тепла - нагревателя отличается от температуры теплоприемника - холодильника на бесконечно малую величину. Термодинамически обратимые процессы могут протекать лишь бесконечно медленно, поскольку предполагается, что система в ходе таких процессов проходит через непрерывный последовательный ряд равновесных состояний. При обратимом протекании процесса работа является максимальной. В необратимом процессе нет возможности возвращения системы в исходное состояние через те же самые промежуточные состояния. Работа и теплота процесса зависит от того, как протекает процесс (обратимо или необратимо). Теплота процесса, равная, согласно I началу термодинамики
в обратимом процессе будет больше, чем в необратимом
поскольку
Все самопроизвольные процессы протекают необратимо.
2. 3. 2. Математическое выражение второго начала термодинамики. Энтропия. Математическая формулировка второго начала термодинамики возникла при анализе работы тепловых машин в трудах Н. Карно и Р. Клаузиуса. Клаузиусом была введена функция состояния S, названная энтропией, изменение которой равно теплоте обратимого процесса, отнесенной к температуре
Так как
Для любого процесса
Полученное выражение представляет собой математическое выражение второго начала термодинамики.
2. 3. 2. 1. Энтропия и термодинамическая вероятность Значение всех термодинамических параметров (давления, температуры, концентрации, плотности и др.) являются усредненным результатом беспорядочного (хаотичного) движения бесконечно большого числа частиц, из которых образованы все тела. Эти параметры теряют смысл в применении к одной или нескольким частицам. Термодинамическую систему можно рассматривать как с точки зрения ее макросостояния, характеризуемого значениями макропараметров (Р - давления, Т - температуры, V - объёма, С -концентрации), так и с позиций ее микросостояния, задаваемого координатами и скоростями движения отдельных частиц, составляющих систему. Одно и то же макросостояние можно реализовать различным набором микросостояний. В термодинамике используется понятие термодинамической вероятности (W), которая равна числу микросостояний, отвечающих данному макросостоянию. Понятно, что в отличие от математической вероятности, которая всегда меньше или равна единице, термодинамическая вероятность меньше единицы быть не может, т. е. W ≥ 1, и является целым и при обычных температурах очень большим числом. Чем больше микросостояний соответствующих данному макросостоянию, тем больше хаотичность (беспорядок) в системе. Энтропию с термодинамической вероятностью связывает уравнение Больцмана:
где k – константа Больцмана. Из уравнения Больцмана следует, что чем больше хаотичность в системе, тем больше энтропия. Таким образом, энтропия характеризует степень неупорядоченности в системе.
2. 3. 2. 2. Изменение энтропии как критерий направления процессов. Для изолированной системы δ Q = 0, поэтому dS ≥ 0. Всякий реальный самопроизвольный процесс всегда является необратимым и для него dS > 0 Следовательно, энтропия может играть роль критерия для выбора направления протекания самопроизвольного процесса. Если изменение энтропии для процесса в изолированной системе больше нуля (энтропия возрастает), то такой процесс может протекать самопроизвольно. Самопроизвольный процесс приводит систему в состояние равновесия, и энтропия при этом достигает своего максимального значения. Таким образом, введение в термодинамику энтропии как функции состояния, позволяет сделать очень важный вывод, который следует из математической формулировки второго начала термодинамики:
|

 ,
,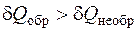 ,
,



 ,
,


