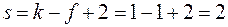Однокомпонентные системы
В зависимости от условий в однокомпонентной системе – индивидуальном веществе – могут сосуществовать одна, две или три устойчивые фазы. Например, при определенных условиях в воде могут находиться в равновесии жидкая вода и газообразная вода (водяной пар) или лед, жидкая вода и пары воды. В однокомпонентной системе, состояние которой определяется двумя параметрами – давлением и температурой – число фаз в равновесии не может быть больше 3. Покажем это с помощью правила фаз Гиббса при k = 1:
откуда
Максимальное число фаз получим при s = 0, следовательно
Наибольший практический интерес представляют двухфазные равновесные системы.
4. 4. 1. Уравнение Клапейрона-Клаузиуса Химический потенциал индивидуального вещества тождественен изобарно-изотермическому потенциалу одного моля вещества. При этом условие двухфазного равновесия
принимает вид
При дифференцировании получаем:
Так как
то
После преобразований
получаем
Так как при фазовом превращении (ф.п.)
то
Это уравнение называют уравнением Клапейрона-Клаузиуса в дифференциальной форме. Оно связывает производную давления по температуре
4. 4. 1. 1. Применение уравнения Клапейрона-Клаузиуса к процессу плавления Плавление – это переход из твердого состояния в жидкое. В этом случае уравнение Клапейрона-Клаузиуса используют для анализа влияния давления на температуру плавления, поэтому его записывают в виде:
Характер изменения температуры плавления от давления определяется знаком производной Однако, имеется небольшое число веществ (вода, висмут, галлий, серый чугун), для которых наблюдается иная (аномальная) зависимость температуры плавления от давления. У этих веществ при плавлении происходит уменьшение объема, а при кристаллизации – увеличение. Всем хорошо известно, что при замерзании воды ее объем увеличивается настолько, что в замкнутой системе происходит разрыв даже стальных и чугунных труб. Для этих веществ Δ V пл. < 0 и, следовательно,
4. 4. 1. 2. Применение уравнения Клапейрона-Клаузиуса к процессам испарения и возгонки Испарение – это процесс перехода из жидкого состояния в газообразное. Газ, полученный испарением жидкости, называют паром. Изменение молярного объема при испарении представляет собой разность между объемом 1 моля вещества в парообразном и в жидком состоянии: Δ V исп. = V пар – V ж. В одинаковых условиях молярный объем любого вещества в паровой фазе во много раз больше, чем объем 1 моля в жидком виде. Например, объем 1 моля воды в парообразном состоянии при температуре кипения (373 К) стандартном давлении (101, 320 кПа) составляет 30, 6 л, как легко рассчитать из уравнения Менделеева-Клапейрона. В жидком же состоянии при этих условиях 1 моль воды занимает объем 18, 8 см3. Поэтому можно считать, что Δ V исп. = V пар – V ж. ≈ V пар Из уравнения Менделеева-Клапейрона
для 1 моля вещества (n = 1) V пар = RT / P Тогда уравнение Клаузиуса –Клапейрона для процесса испарения примет вид:
или
Разделим переменные и проинтегрируем
При температурах, далеких от критической температуры, можно считать, что теплота испарения не зависит от температуры, тогда
и
Полученное уравнение является уравнением Клаузиуса-Клапейрона в интегральной форме. Оно описывает зависимость давления насыщенного пара от температуры. Насыщенным называется пар, находящийся в равновесии с жидкостью. Данное уравнение можно представить в виде
где коэффициент A равен константе интегрирования (A = const), а Из этого уравнения видно, что график зависимости ln P = f(1/T) представляет собой прямую линию, из тангенса угла наклона которой можно найти теплоту испарения (рис. 4).
Рис.4. Зависимость логарифма давления насыщенного пара от обратной температуры.
tgα = – B, а Δ H исп. = BR Для процесса возгонки – перехода из твердого состояния в газообразное – интегральная форма уравнения Клапейрона-Клаузиуса имеет аналогичный вид:
так как молярный объем любого вещества в твердом состоянии много меньше молярного объема вещества в газообразном состоянии и выполняется соотношение Δ V возг. = V газ – V тв. ≈ V газ. 4. 4. 2. Диаграмма состояния однокомпонентной системы Зависимость давления от температуры для различных фазовых превращений в равновесных условиях, вытекающие из уравнения Клаузиуса- Клапейрона, могут быть представлены в виде диаграммы состояния однокомпонентной системы. На рис. 5 в качестве примера приведена диаграмма состояния воды.
Рис. 5. Диаграмма состояния воды в области невысоких давлений (приведена схематично без соблюдения масштаба).
На диаграмме видны: - три области давлений и температур, при которых устойчиво существуют твердая (лед), жидкая и газообразная фазы; - три линии, разделяющие эти области и отвечающие равновесному сосуществованию твердой и жидкой фаз (кривая плавления OB), твердой и газообразной фаз (кривая возгонки OA), жидкой и газообразной (парообразной) фаз (кривая испарения OK); - точка O, в которой сходятся три линии, что соответствует равновесному сосуществованию трех фаз – твердой, жидкой и газообразной – так называемая, тройная точка. Рассчитаем число степеней свободы в состоянии, которому соответствует точка O:
т. е. система нонвариантна. Это означает, что существуют только одно определенное значение температуры (273, 16 К) и одно определенное значение давление насыщенного пара воды (610 Па), при которых сосуществуют три фазы. Изменение хотя бы одного из параметров – температуры или давления – приводит к изменению числа фаз в системе. Так как сосуществованию трех фаз соответствует строго определенная температура, тройную точку воды используют для создания эталона температуры. Первичный государственный эталон температуры хранится в Санкт-Петербурге во Всероссийском научно-исследовательском институте метрологии им. Д. И. Менделеева. В любой точке, лежащей на линиях, соответствующих равновесию между двумя фазами, число степеней свободы равно:
Это означает, что, сохраняя двухфазное равновесие, независимо можно менять только один параметр – или давление, или температуру. Второй параметр будет изменяться в соответствии с уравнением Клаузиуса-Клапейрона. Точки на диаграмме состояния, лежащие в областях существования одной из фаз – льда, жидкой воды или пара – отвечают состояниям системы с числом термодинамических степеней свободы
|
,
,
,
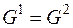
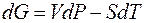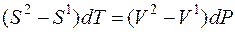
с теплотой перехода одного моля вещества из первой фазы во вторую Δ H ф.п. и изменением молярного объема при фазовом переходе Δ V ф.п. при температуре фазового превращения. Полученное уравнение Клапейрона-Клаузиуса является универсальным уравнением, применимым к любому двухфазному равновесию. Рассмотрим применение уравнения Клапейрона- Клаузиуса к различным фазовым переходам, имеющим практическое значение.
. Так как T пл. > 0и Δ H пл. > 0, то знак производной определяется знаком Δ V пл.. Для большинства веществ объем при плавлении увеличивается Δ V пл. > 0 и, следовательно, 
,
,
,
,
