Трехкомпонентные системы
Из анализа уравнения правили фаз s = k – f + 2 следует, что в трех компонентной системе при k = 3 максимальное число сосуществующих фаз (при s = 0) равно 5, а максимальная вариантность системы (при f min = 1) s max = 3 – 1 + 2 = 4. Это значит, что для полной характеристики системы, даже не учитывая объема, следует задать четыре параметра: температуру, давление и содержание двух компонентов. Чтобы графически изобразить такую систему, нужно четыре координатные оси. На практике для трехкомпонентных систем соотношения между составом системы, числом и видом фаз изучают при постоянстве и температуры и давлении, изображая состав системы в виде равносторонних или прямоугольных треугольников (методы Гиббса и Розебома).
4. 7. 1. Закон распределения При рассмотрении растворимости жидкостей в трехкомпонентной системе было обнаружено, что добавление к двум практически нерастворимым или ограниченно растворимым жидкостям A и B третьего компонента C увеличивает их взаимную растворимость. При этом концентрация компонента C в сосуществующих жидких слоях неодинакова. Так как анализировать закономерности, выраженные диаграммами состояния в тройных системах, весьма сложно, перейдем к математическим уравнениям. Это позволит обнаружить практически важные зависимости. Как известно (см. разд. 4. 2), признаком равновесия в гетерогенной системе является равенство химических потенциалов компонентов во всех сосуществующих фазах. Применим это условие к веществу C в двухфазной жидкой системе. Химические потенциалы C в фазе 1 и в фазе 2 выразим через активность a компонента C (см. разд. 2. 3. 4.):
Так как
откуда
Стандартные химические потенциалы при данной температуре величины постоянные, их разность тоже постоянна, поэтому
или
Полученную закономерность называют законом распределения, а константу K – коэффициентом распределения. Закон распределения выполняется при условии, что добавление компонента C не изменяет в заметной степени взаимную растворимость A и B. Для достаточно разбавленных растворов вместо отношения активностей можно использовать отношение молярных долей или концентраций:
4. 7. 2. Экстрагирование На законе распределения основан один из важных методов разделения веществ – экстрагирование (экстракция). Он заключается в извлечении вещества из раствора подходящим растворителем (экстрагентом), который не смешивается с исходным раствором. Конечно, экстрагент должен растворять извлекаемое вещество в большем количестве, чем исходный растворитель, т.е. коэффициент распределения должен заметно отличаться от единицы. Для увеличения степени извлечения экстрагируемое вещество целесообразно переводить в то молекулярное состояние, которое характерно для обеих равновесных фаз. Например, при извлечении слабой органической кислоты выгодно добавлением минеральной кислоты понизить степень ее диссоциации. Тогда недиссоциированные молекулы органической кислоты будут извлечены более полно. Растворимость органических веществ в воде значительно уменьшается в присутствии солей (эффект «высаливания»), что также широко используют для увеличения полноты извлечения. Экстрагирование целесообразно вести последовательно несколькими порциями экстрагента. При этом количество извлеченного вещества на единицу объема экстрагента больше, чем при однократной экстракции. Установки для промышленного экстрагирования напоминают ректификационные колонны, а сам процесс экстракции нередко сочетают с ректификацией.
|



 , то
, то ,
, .
.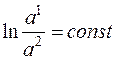
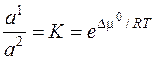
 ;
; 



