Количество информации, получаемой в процессе сообщения
До сих пор мы приводили формулы для расчета энтропии (неопределенности) H, указывая, что H в них можно заменять на I, потому что количество информации, получаемое при полном снятии неопределенности некоторой ситуации, количественно равно начальной энтропии этой ситуации. Но неопределенность может быть снята только частично, поэтому количество информации I, получаемой из некоторого сообщения, вычисляется как уменьшение энтропии, произошедшее в результате получения данного сообщения.
Для равновероятного случая, используя для расчета энтропии формулу Хартли, получим:
Второе равенство выводится на основании свойств логарифма. Таким образом, в равновероятном случае I зависит от того, во сколько раз изменилось количество рассматриваемых вариантов выбора (рассматриваемое разнообразие). Исходя из (5) можно вывести следующее: Если Если Если Если количество рассматриваемых альтернатив в результате получения сообщения уменьшилось вдвое, т.е. Рассмотрим в качестве примера опыт с колодой из 36 карт.
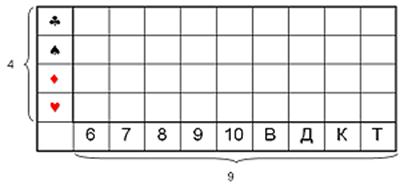
Рис. 12. Иллюстрация к опыту с колодой из 36-ти карт. Пусть некто вынимает одну карту из колоды. Нас интересует, какую именно из 36 карт он вынул. Изначальная неопределенность, рассчитываемая по формуле (2), составляет H=log2(36)@5, 17 бит. Вытянувший карту сообщает нам часть информации. Используя формулу (5), определим, какое количество информации мы получаем из этих сообщений:
Вариант A. “Это карта красной масти”. I=log2(36/18)=log2(2)=1 бит (красных карт в колоде половина, неопределенность уменьшилась в 2 раза).
Вариант B. “Это карта пиковой масти”. I=log2(36/9)=log2(4)=2 бита (пиковые карты составляют четверть колоды, неопределенность уменьшилась в 4 раза).
Вариант С. “Это одна из старших карт: валет, дама, король или туз”. I=log2(36)–log2(16)=5, 17-4=1, 17 бита (неопределенность уменьшилась больше чем в два раза, поэтому полученное количество информации больше одного бита).
Вариант D. “Это одна карта из колоды";. I=log2(36/36)=log2(1)=0 бит (неопределенность не уменьшилась - сообщение не информативно).
Вариант D. “Это дама пик";. I=log2(36/1)=log2(36)=5, 17 бит (неопределенность полностью снята). Задачи 1. Априори известно, что шарик находится в одной из трех урн: А, В или С. Определите, сколько бит информации содержит сообщение о том, что он находится в урне В. Варианты: 1 бит, 1, 58 бита, 2 бита, 2, 25 бита. 2. Вероятность первого события составляет 0, 5, а второго и третьего 0, 25. Чему для такого распределения равна информационная энтропия. Варианты: 0, 5 бита, 1 бит, 1, 5 бита, 2 бита, 2, 5 бита, 3 бита. 3. Вот список сотрудников некоторой организации:
Определите количество информации, недостающее для того, чтобы выполнить следующие просьбы: a) Пожалуйста, позовите к телефону Иванову. b) Меня интересует одна ваша сотрудница, она 1970 года рождения. 4. Какое из сообщений несет больше информации: - В результате подбрасывания монеты (орел, решка) выпала решка. - На светофоре (красный, желтый, зеленый) сейчас горит зеленый свет. - В результате подбрасывания игральной кости (1, 2, 3, 4, 5, 6) выпало 3 очка. Чему равно количество информации, получаемое в каждом из этих сообщений. 5. Загадано произвольное трехзначное десятичное число. A) Чему равна исходная неопределенность? B) Какое количество информации вы получите, узнав, какая цифра находится в одной из позиций этого числа? C) Чему будет равна оставшаяся после этого неопределенность?
6. Какое из сообщений снимает большую неопределенность: - Ожидайте слесаря завтра в течение дня; - Ожидайте слесаря завтра до обеда; - Ожидайте слесаря завтра с десяти до одиннадцати.
|

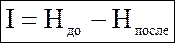 (4)
(4)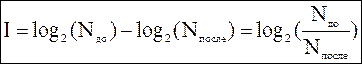 (5)
(5)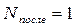 , то
, то 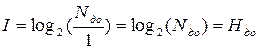 - полное снятие неопределенности, количество полученной в сообщении информации равно неопределенности, которая существовала до получения сообщения.
- полное снятие неопределенности, количество полученной в сообщении информации равно неопределенности, которая существовала до получения сообщения.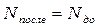 , то
, то 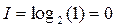 - неопределенности не изменилась, следовательно, информации получено не было.
- неопределенности не изменилась, следовательно, информации получено не было.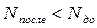 , то
, то 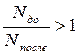 =>
=> 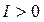 , если
, если 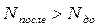 ,
, 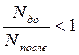 =>
=> 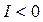 . Т.е. количество полученной информации будет положительной величиной, если в результате получения сообщения количество рассматриваемых альтернатив уменьшилось, и отрицательной, если увеличилось.
. Т.е. количество полученной информации будет положительной величиной, если в результате получения сообщения количество рассматриваемых альтернатив уменьшилось, и отрицательной, если увеличилось.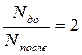 , то I=log2(2)=1 бит. Другими словами, получение 1 бита информации исключает из рассмотрения половину равнозначных вариантов.
, то I=log2(2)=1 бит. Другими словами, получение 1 бита информации исключает из рассмотрения половину равнозначных вариантов.