Формула Шеннона

В общем случае, энтропия H и количество получаемой в результате снятия неопределенности информации I зависят от исходного количества рассматриваемых вариантов N и априорных вероятностей реализации каждого из них P: {p₀, p₁, …p_N-1}, т.е. H=F(N, P). Расчет энтропии в этом случае производится по формуле Шеннона, предложенной им в 1948 году в статье " Математическая теория связи".

В частном случае, когда все варианты равновероятны, остается зависимость только от количества рассматриваемых вариантов, т.е. H=F(N). В этом случае формула Шеннона значительно упрощается и совпадает с формулой Хартли, которая впервые была предложена американским инженером Ральфом Хартли в 1928 году, т.е. на 20 лет раньше.

 

Формула Шеннона имеет следующий вид:

 

(1)

 

Напомним, что такое логарифм.

Рис. 10. Нахождение логарифма b по основанию a - это нахождение степени, в которую нужно возвести a, чтобы получить b.

Логарифм по основанию 2 называется двоичным:

log₂(8)=3 => 2³=8

log₂(10)=3, 32 => 2^{3, 32}=10

Логарифм по основанию 10 –называется десятичным:

 

log₁₀(100)=2 => 10²=100

Основные свойства логарифма:

1. log(1)=0, т.к. любое число в нулевой степени дает 1;

2. log(a^b)=b*log(a);

3. log(a*b)=log(a)+log(b);

4. log(a/b)=log(a)-log(b);

5. log(1/b)=0-log(b)=-log(b).

 

Знак минус в формуле (1) не означает, что энтропия – отрицательная величина. Объясняется это тем, что p_i£ 1 по определению, а логарифм числа меньшего единицы - величина отрицательная. По свойству логарифма , поэтому эту формулу можно записать и во втором варианте, без минуса перед знаком суммы.

интерпретируется как частное количество информации , получаемое в случае реализации i-ого варианта. Энтропия в формуле Шеннона является средней характеристикой – математическим ожиданием распределения случайной величины {I₀, I_1, … I_N-1}.

Приведем пример расчета энтропии по формуле Шеннона. Пусть в некотором учреждении состав работников распределяется так: ¾ - женщины, ¼ - мужчины. Тогда неопределенность, например, относительно того, кого вы встретите первым, зайдя в учреждение, будет рассчитана рядом действий, показанных в таблице 2.

Таблица 2.

	pi	1/pi	Ii=log2(1/pi), бит	pi*log2(1/pi), бит
Ж	3/4	4/3	log2(4/3)=0, 42	3/4 * 0, 42=0, 31
М	1/4	4/1	log2(4)=2	1/4 * 2=0, 5
å	1			H=0, 81 бит

 

Если же априори известно, что мужчин и женщин в учреждении поровну (два равновероятных варианта), то при расчете по той же формуле мы должны получить неопределенность в 1 бит. Проверка этого предположения проведена в таблице 3.

Таблица 3.

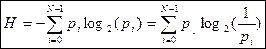	pi	1/pi	Ii=log2(1/pi), бит	pi*log2(1/pi), бит
Ж	1/2		log2(2)=1	1/2 * 1=1/2
М	1/2		log2(2)=1	1/2 * 1=1/2
å	1			H=1 бит