РАСЧЕТ ПУСКОВЫХ ХАРАКТЕРИСТИК
Известно, что с увеличением частоты тока в стержнях обмотки короткозамкнутого ротора возникает эффект вытеснения тока, в результате которого плотность тока в верхней части стержней возрастает, а в нижней – уменьшается, при этом активное сопротивление ротора увеличивается, а индуктивное – уменьшается. Изменение сопротивлений ротора влияет на пусковые характеристики машины. В большинстве случаев эффект вытеснения тока в обмотках короткозамкнутых роторов играет положительную роль, так как увеличивает начальные моменты двигателей. Это широко используют при проектировании асинхронных машин, выполняя роторы с глубокими прямоугольными или фигурными пазами или с двойной беличьей клеткой, в которых эффект вытеснения тока проявляется особенно сильно. Однако неравномерное распределение плотности тока по сечению стержня ротора может привести и к нежелательным последствиям. Например, при неудачно выбранных размерных соотношениях стержней чрезмерно возрастающая в пусковых режимах плотность тока в их верхних участках может вызвать неравномерное тепловое удлинение стержней и их изгиб. При этом стержни разрывают усики пазов и выгибаются в воздушный зазор, что неизбежно приводит к выходу двигателя из строя. В связи с этим правильный учет влияния эффекта вытеснения тока является необходимым при проектировании асинхронных машин с короткозамкнутыми роторами. В расчетах оказалось удобнее определять не непосредственно активное и индуктивное сопротивления стержней при неравномерной плотности тока, а их относительные изменения под действием эффекта вытеснения тока. Эти изменения оценивают коэффициентами kr и k д. Коэффициент k r показывает, во сколько раз увеличилось активное сопротивление пазовой части стержня r cξ при неравномерной плотности тока в нем по сравнению с его сопротивлением rс при одинаковой плотности по всему сечению стержня:
Коэффициент демпфирования k д показывает, как уменьшилась магнитная проводимость λ Пξ участка паза, занятого проводником с током, при действии эффекта вытеснения тока по сравнению с проводимостью того же участка, но при равномерной плотности тока в стержне λ 'п:
Аналитическими выражениями, определяющими kr и k Д, полученными для прямоугольных стержней при допущениях о постоянстве удельного сопротивления материала стержня по всей площади его поперечного сечения, бесконечности магнитной проницаемости стали магнитопровода и прямолинейности магнитных линий потока рассеяния в пазу, являются
В этих выражениях ξ, так называемая " приведенная высота" стержня, — величина безразмерная, значение которой определяется по формуле
где h c - высота стержня в пазу, м: hc = h п -(h ш + h' ш); bс и b п - ширина стержня и ширина паза, м. При расчете роторов со вставными стержнями принимают bc = 0, 9 b П; в роторах с литой обмоткой bc = b П; f 2 — частота тока в роторе в расчетном режиме, Гц; р cυ — удельное сопротивление материала стержня при расчетной температуре, Ом · м. Для двигателей общего назначения с медными вставными стержнями короткозамкнутого ротора при расчетной температуре 75°С (рс75 = 10-6/47 Ом· м,) из (10.4) имеем
При расчетной температуре 115°С (rс75=10-6/47Ом× м)
При литой алюминиевой обмотке ротора при расчетных температурах 75°С (рс75=10-6/21, 5 Ом· м) и 115˚ С (pcll5 = 10-6/20, 5 Ом· м) соответственно имеем
Анализ зависимостей (10.3) показывает, что при ξ < 1 эффект вытеснения тока практически не влияет на сопротивления стержней. Это является критерием необходимости его учета при проектировании. В расчетах условно принимают, что при действии эффекта вытеснения ток ротора распределен равномерно, но не по всему сечению стержня, а лишь по его верхней части, ограниченной высотой hr, имеющей сечение qr и сопротивление r cξ = rcqc/qr, h r называют глубиной проникновения тока в стержень. Для прямоугольных стержней hr = hc /kr. При определении λ Пξ аналогично принимают, что ток равномерно распределен по верхней части сечения стержня высотой hx.
В практических расчетах для определения kr и k д пользуются не аналитическими зависимостями (10.3), а построенными на их основе кривыми φ (ξ) и φ ΄ (ξ) (рис. 10.1 и 10.2). Принятые при выводе (10.3) допущения приводят к положению, что на глубину проникновения не влияют высота и конфигурация стержня. Это позволяет использовать (10.3) и кривые φ (ξ) и φ ΄ (ξ) для определения kr и k д в стержнях различных конфигураций. Расчет проводят в следующей последовательности. По полной высоте стержня, частоте тока и удельному сопротивлению материала стержня по (10.4) определяют функцию ξ, в соответствии с которой по кривым рис. 10.1 находят функцию φ, а по кривым рис. 10.2 — функцию φ '. Рис. 10.1. Кривые j и jКР в функции «приведенной высоты» x (j»x-1 приx> 4 и j=0, 089x4 при x< 1)
Далее определяют глубину проникновения тока
и коэффициент k д = φ '. Коэффициент kr находят по отношению площадей всего сечения стержня и сечения, ограниченного высотой hr, т.е.
Рис.10.2. Зависимость j¢ от «приведенной высоты» x; при x> 4 и j¢ =3/2x
По значениям kr и k Д можно найти сопротивление пазовой части стержня обмотки ротора и коэффициент магнитной проводимости участка паза ротора, занятого стержнем с током:
Для определения kr в стержнях некоторых наиболее распространенных конфигураций используют заранее полученные расчетные формулы Для прямоугольных стержней (рис. 10.3, а)
Для круглых стержней (рис. 10.3, б)
Функция φ КР для круглого стержня представлена на рис. 10.1. Для грушевидных стержней (рис. 10.3, в)
здесь (10.15)
Площадь сечения qr при
где
При hr≤ b1 /2 площадь
При hr > h 1+ b 1/2 принимают qr≈ qc и kr = 1. Для трапецеидальных стержней с узкой верхней частью (см. рис. 10.3, г)
qc определяют по (10.15). Площадь qr при hr ≤ b1 /2 определяют по (10.17) и при hr ≥ b1 /2 – по (10.16), причем
Рис. 10.3. К расчету kr в стержнях различной конфигурации: hr - расчетная глубина проникновения тока
Для других конфигураций стержней kr может быть определен из общего выражения kr =qc/qr с учетом размерных соотношений стержня и глубины проникновения тока в стержень hr. Для расчета характеристик необходимо учитывать изменение сопротивления всей обмотки ротора r2, поэтому удобно ввести коэффициент общего увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока:
где r 2ξ – сопротивление фазы короткозамкнутого ротора с учетом влияния эффекта вытеснения тока. Выражение (10.19) легко преобразовать в более удобный для расчета вид:
Для прямоугольных стержней это выражение приобретает вид
В (10.20) и (10.21) для роторов без радиальных вентиляционных каналов с литой обмоткой (с прилегающими замыкающими кольцами) rc'=rc. Для роторов с радиальными вентиляционными каналами и роторов с отставленными замыкающими кольцами
где lс — полная длина стержня, равная расстоянию между замыкающими кольцами, м; nК и bК — число и ширина, м, радиальных вентиляционных каналов; l 2 — длина сердечника ротора, м. Активное сопротивление фазы обмотки ротора с учетом вытеснения тока будет равно:
Обозначив коэффициентом Кх изменение индуктивного сопротивления фазы обмотки ротора от действия эффекта вытеснения тока, получим
тогда
где λ Пξ - коэффициент магнитной проводимости пазового рассеяния с учетом эффекта вытеснения тока:
здесь
λ ΄ П2 – коэффициент магнитной проводимости участка паза, занятого проводником с обмоткой (выражение для определения λ 'П2 в формулах табл. 7.5 является множителем перед коэффициентом k д). Выше рассматривались методы расчета параметров при допущении отсутствия насыщения стали магнитопровода полями рассеяния, магнитная проницаемость которой принималась равной бесконечности. При расчетах параметров холостого хода и рабочих режимов это допущение вполне оправдано, так как токи в этих режимах относительно малы и потоки рассеяния не создают заметного падения магнитного напряжения в стали зубцов. При увеличении скольжения свыше критического и в пусковых режимах токи в обмотках возрастают и потоки рассеяния увеличиваются. Коронки зубцов статора ротора в машинах средней и большой мощности в большинстве случаев оказываются сильно насыщенными.
Уменьшение потока пазового рассеяния из-за насыщения приближенно учитывают введением дополнительного раскрытия паза, равного с э. Дополнительное раскрытие с э принимается таким, чтобы его магнитное сопротивление потоку рассеяния было равно магнитному сопротивлению насыщенных участков зубцов. При этом условии можно использовать для расчета коэффициент магнитной проводимости паза с учетом насыщения обычные формулы, предполагая, что μ ст = ∞. Уменьшение λ п из-за насыщения участков зубцов (Δ λ п.нас) будет определяться с э. Таким образом, с э зависит от уровня насыщения верхней части зубцов потоками рассеяния и, следовательно, от МДС паза, т.е. от тока в обмотке. Так как ток обмотки в свою очередь зависит от индуктивного сопротивления, определяемого магнитной проводимостью, то расчет приходится проводить методом последовательных приближений. Первоначально задаются предполагаемой кратностью увеличения тока, обусловленной уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны:
где I - ток, рассчитанный для данного режима без учета насыщения; I нас — ток в этом же режиме работы машины при насыщении участков зубцов полями рассеяния. Ориентировочно для расчета пусковых режимов принимают k нас=1, 25÷ 1, 4; для режима максимального момента k нас = 1, 1 ÷ 1, 2. Для двигателей с открытыми пазами следует задаваться меньшими значениями k нас, при полузакрытых пазах - большими. Расчет проводят в следующей последовательности. Определяют среднюю МДС обмотки, отнесенную к одному пазу обмотки статора:
где I 1 — ток статора, соответствующий расчетному режиму, без учета насыщения; а — число параллельных ветвей обмотки статора; uп1 — число эффективных проводников в пазу статора; k 'β — коэффициент, учитывающий уменьшение МДС паза, вызванное укорочением шага обмотки, рассчитывается по (7.25) или по (7.26); k yl — коэффициент укорочения шага обмотки. По средней МДС F п.cр рассчитывают фиктивную индукцию потока рассеяния в воздушном зазоре, Тл:
где коэффициент
(tZ 1 и tZ 2 - зубцовые деления статора и ротора).
По полученному значению B δ ф определяют отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом κ δ , значение которого находят по кривой рис.10.5. Далее рассчитывают значения дополнительного эквивалентного раскрытия пазов статора и ротора (с э1 и с э2), магнитные напряжения которых будут эквивалентны МДС насыщенных участков усиков зубцов. Для пазов статора его принимают равным:
Вызванное насыщением от полей рассеяния уменьшение коэффициента магнитной проводимости рассеяния открытого паза (рис.10.6, а)
Для полуоткрытых и полузакрытых пазов расчетная формула несколько усложняется из-за более сложной конфигурации их верхних клиновых частей. Для полуоткрытого паза (рис. 10.6, б)
Рис. 10.6. К расчету влияния насыщения потоком рассеяния на коэффициент магнитной проводимости паза: а—ж — различные конфигурации верхней части пазов
Для полузакрытого паза (рис. 10.6, в, г)
Для фазных и короткозамкнутых роторов дополнительное раскрытие рассчитывают по формуле
Уменьшение коэффициента проводимости для открытых и полузакрытых пазов ротора (рис. 8.62, д—ж)
Коэффициент магнитной проводимости пазового рассеяния при насыщении λ П1нас определяют для статора из выражения
где λ П1 — проводимость, рассчитанная без учета насыщения. Для ротора
где lП2x — проводимость пазового рассеяния ротора для ненасыщенной зубцовой зоны с учетом влияния вытеснения тока. Коэффициенты проводимости дифференциального рассеяния при насыщении участков зубцов статора lД1нас и ротора lД2нас
Значения χ d принимают по кривым рис. 10.5.
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния определяют по отношению сумм коэффициентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния:
Для ротора принимают отношения сумм проводимостей, рассчитанных без учета влияния насыщения и действия эффекта вытеснения тока (для номинального режима) и с учетом этих факторов:
Значения параметров x 1 нас и x 2x нас используют при расчете точек характеристик при скольжениях s ³ s kр. Полученные для каждой из точек характеристики отношения токов, рассчитанных с учетом и без учета насыщения, сравнивают с принятыми коэффициентами k нас. Если расхождение превышает 5—8%, то расчет для этого значения s повторяют, внося соответствующую корректировку в первоначально принимаемый коэффициент k нас. Пусковые свойства асинхронных двигателей характеризуются начальным пусковым и максимальным моментами и начальным пусковым током. В двигателях с фазными роторами начальный момент и пусковой ток определяются сопротивлением пускового реостата. В двигателях с короткозамкнутыми роторами значения моментов и начального тока зависят от соотношений параметров. Кроме того, важным показателем пусковых свойств короткозамкнутого двигателя является значение минимального момента. Уменьшение момента в процессе разгона двигателя может произойти в связи с изменением соотношения параметров при уменьшении скольжения. Стандарты на асинхронные двигатели устанавливают наименьшие допустимые относительные значения моментов и наибольшие относительные значения начальных пусковых токов для выпускаемых асинхронных машин в зависимости от их мощности, исполнения и числа пар полюсов.
Таблица 10.1 Кратность начальных пусковых моментов MП* и токов I П* асинхронных двигателей
Примечание. Некоторые двигатели малой мощности с высотой оси вращения h£ 80 мм выполняются с уменьшенной кратностью начального пускового тока.
Для короткозамкнутых двигателей регламентируются значения всех перечисленных выше моментов и тока, а для двигателей с фазными роторами – только значения максимальных моментов, т. е. перегрузочная способность двигателей. В табл. 10.1 приведены допустимые относительные значения моментов и начального пускового тока двигателей с короткозамкнутыми роторами серии 4А. Спроектированная заново асинхронная машина на базе серии 4А должна иметь пусковые характеристики, удовлетворяющие этим требованиям. В технических условиях или в заданиях на проектирование специальных асинхронных двигателей могут быть поставлены более жесткие требования к этим величинам. В практике расчетов часто ограничиваются определением только двух точек характеристик: начального пускового и максимального моментов и начального пускового тока. Такой расчет дает лишь приближенные сведения о пусковых свойствах двигателя и может привести к погрешности при определении перегрузочной способности из-за неточности определения критического скольжения. Поэтому при проектировании целесообразно рассчитывать полные пусковые характеристики, т.е. зависимости М* = f(s) и I* = f(s) для всего диапазона изменения скольжений от s = 1 до значения, соответствующего режиму, близкому к номинальному. Расчет пусковых характеристик затруднен необходимостью учета изменений параметров, вызванных эффектом вытеснения тока и насыщением от полей рассеяния, так как при больших скольжениях токи в обмотках статора и ротора короткозамкнутых двигателей могут превышать свое минимальное значение в 7—7, 5 раза (табл. 10.1). В то же время при больших токах увеличивается падение напряжения на сопротивлении обмотки статора, что вызывает уменьшение ЭДС и снижение основного потока. Для учета этих факторов необходимо применение ЭВМ. При ручном счете используют следующий упрощенный метод. Учитывая, что индуктивное сопротивление взаимной индукции x12 с уменьшением насыщения магнитопровода увеличивается, в расчете пусковых характеристик для скольжений s ³ 0, 1 ¸ 0, 15 оно может быть принято равным
Не внося большой погрешности, в расчетных формулах пусковых режимов пренебрегают сопротивлением r 12. Это оправдано при токах, заметно превышающих номинальный, так как электрические потери в обмотках, возрастающие пропорционально квадрату тока, многократно превышают потери в стали, для учета которых в схему замещения введен параметр r 12. При этих допущениях коэффициент
и сопротивление правой ветви Г-образной схемы замещения (см. рис.9.1)
где для упрощения расчетных формул в отличие от обозначений в расчете рабочих характеристик принято
Ток в обмотке ротора
Сопротивление всей схемы замещения для пусковых режимов
Из (10.42) - (10.45) следует
Полученные выражения (10.44) — (10.47) дают возможность рассчитать токи и моменты во всем диапазоне изменения скольжения от s = 1 до s = 0, 1.
|

 (10.1)
(10.1) (10.2)
(10.2)
 (10.3)
(10.3) (10.4)
(10.4) (10.5)
(10.5) (10.6)
(10.6)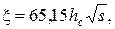 (10.7)
(10.7) (10.8)
(10.8)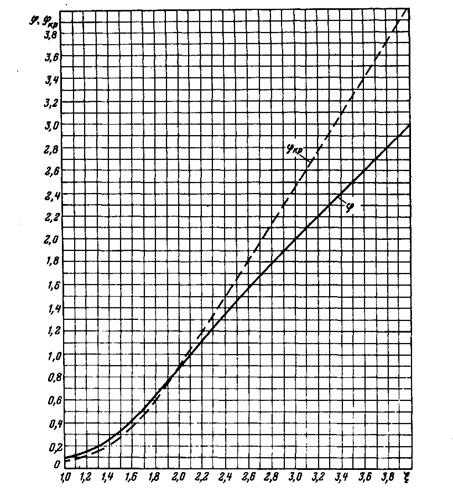
 (10.9)
(10.9) (10.10)
(10.10)
 (10.11)
(10.11) (10.12)
(10.12) (10.13)
(10.13) (10.14)
(10.14)



 (10.16)
(10.16)
 (10.17)
(10.17)
 (10.18)
(10.18)
 (10.19)
(10.19) (10.20)
(10.20) (10.21)
(10.21)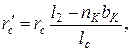 (10.22)
(10.22) (10.23)
(10.23) (10.24)
(10.24) (10.25)
(10.25)

 Насыщение коронок зубцов (рис. 10.4) приводит к увеличению магнитного сопротивления для части потока рассеяния, магнитные линии которого замыкаются через верхнюю часть паза. Поэтому коэффициент магнитной проводимости пазового рассеяния уменьшается. Несколько снижается также магнитная проводимость дифференциального рассеяния. На коэффициент магнитной проводимости лобового рассеяния насыщение стали потоками рассеяния влияния не оказывает.
Насыщение коронок зубцов (рис. 10.4) приводит к увеличению магнитного сопротивления для части потока рассеяния, магнитные линии которого замыкаются через верхнюю часть паза. Поэтому коэффициент магнитной проводимости пазового рассеяния уменьшается. Несколько снижается также магнитная проводимость дифференциального рассеяния. На коэффициент магнитной проводимости лобового рассеяния насыщение стали потоками рассеяния влияния не оказывает.

 (10.26)
(10.26) (10.27)
(10.27) (10.28)
(10.28) (10.29)
(10.29) (10.30)
(10.30) (10.31)
(10.31)
 (10.32)
(10.32) (10.33)
(10.33)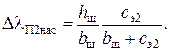 (10.34)
(10.34) (10.35)
(10.35) (10.36)
(10.36)
 (10.37)
(10.37) (10.38)
(10.38) (10.39)
(10.39) (10.40)
(10.40) (10.41)
(10.41) (10.42)
(10.42)
 (10.43)
(10.43) (10.44)
(10.44) (10.45)
(10.45) (10.46)
(10.46) Характеризующие пусковые данные машины кратность тока и момента при заданном s
Характеризующие пусковые данные машины кратность тока и момента при заданном s (10.47)
(10.47)


