Решение. Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе
C 1U 1 = C 2U 2. С другой стороны, U 1 + U 2 = U. Решая совместно эту систему уравнений, найдем напряжение на первом и втором конденсаторе
Подставляя эти значения в формулу для энергии конденсатора, получим
Подставим значения величин и получим WЭ1 = 2× 10-6 Дж = 2 мкДж, WЭ2 = 1× 10-6 Дж = 1 мкДж. 6. Медный проводник (удельное сопротивление меди r = 17 нОм·м) подключен к источнику с ЭДС, e = 4 В. Внутреннее сопротивление источника r = 0, 1 Ом. Сечение проводника S = 0, 085 мм2, длина l = 9, 5 м. Считая, что ток течет по всему поперечному сечению проводника, найти величину напряженности электрического поля внутри него.
Чтобы найти напряженность электрического поля в проводнике, воспользуемся законом Ома в дифференциальной форме: j = sE, где j – плотность тока; E – вектор напряженности электрического поля; s – электропроводность вещества проводника, равная 1/ r. Величина искомой напряженности электрического поля в проводнике определяется соотношением: E = j / s = rj. (1) Таким образом, задача нахождения напряженности поля сводится к задаче нахождения величины плотности тока j в цепи. Плотность тока можно найти, если известна сила тока I, протекающего по проводнику j = I / S. (2) Полный ток в цепи найдем из закона Ома для полной цепи: I = e / (R + r), (3) где r – внутреннее сопротивление источника; R - сопротивление проводника. Для R справедливо соотношение: R = rl/S. (4) Объединяя формулы (1) - (4), окончательно запишем E = rj = rI / S = re / (R + r)S = re / (rl / S + r)S. (5) Подстановка в (5) численных данных позволяет написать ответ Е = 0, 4 В/м. 7. Падение напряжения в проводнике, состоящем из двух последовательно соединенных кусков медной проволоки одинаковой длины (l 1 = l 2 = 10 м), но разного диаметра (d1 = 2d2), равно 10 В. Найти удельную тепловую мощность тока во втором куске проволоки. Удельное сопротивление меди r = 17 нОм·м.
Удельная тепловая мощность тока (плотность тепловой мощности) w = sE 2 = Поэтому, чтобы найти w2, необходимо определить две величины: количество теплоты Q2, которое выделяется в более тонком проводнике в единицу времени, и объем этого проводника. Количество теплоты Q2 можно найти, если учесть, что ток в проводниках один и тот же, а сопротивления проводников отличаются в 4 раза.
Согласно закону Джоуля-Ленца, представленному в интегральной форме,
где Q1 – тепло, выделяющееся в единицу времени в более толстом проводнике. Общая энергия, которая выделяется во всем проводнике, рассчитывается по формуле
где U –падение напряжения в проводнике. Из уравнения (1) следует, что количество теплоты, выделяющееся во втором проводнике в единицу времени,
В уравнении (2) все величины, кроме сопротивления второго участка проводника, известны. Однако в знании R2 нет необходимости. Действительно, если связать между собой объем второго проводника с его сопротивлением
то нетрудно видеть, что удельная тепловая мощность тока во втором проводнике не зависит от его сопротивления
Подставляя в соотношение (3) численные данные, получаем ответ w 2 = 3, 76× 10 7 Вт/м3. 8. Заряд сферического конденсатора из-за того, что через диэлектрическую прокладку протекает ток, уменьшается за время t в n раз. Найти удельное сопротивление r прокладки, если ее диэлектрическая проницаемость равна e.
Сопротивление диэлектрика между обкладками сферического конденсатора можно найти, просуммировав сопротивления сферических слоев толщиной dr, граничащих друг с другом:
где a, b – радиусы соответственно внутренней и внешней обкладок сферического конденсатора; e0 – электрическая постоянная; C – емкость сферического конденсатора находится по формуле
Из уравнения (1) следует, что для определения величины удельного сопротивления материала прокладки достаточно найти произведение емкости конденсатора на полное сопротивление прокладки:
Это можно сделать, если учесть, что за время dt конденсатор теряет заряд:
где I – ток утечки. Знак «-» в (3) учитывает тот факт, что заряд конденсатора со временем убывает. По закону Ома
где U – разность потенциалов между обкладками конденсатора,
где q – заряд конденсатора. Объединяя формулы (3) – (5), получаем дифференциальное соотношение, в которое входит искомое произведение CR:
После интегрирования получаем
где q1 – начальный заряд конденсатора; q2 – конечный. Подставляя CRиз (6) в (2), окончательно имеем
|

 Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать
Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать ,
, .
. ;
; .
. Решение
Решение Решение
Решение E2 = rj 2.
E2 = rj 2. .
. ,
, , (1)
, (1) . (2)
. (2) ,
,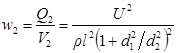 . (3)
. (3) Решение
Решение , (1)
, (1)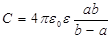 .
. . (2)
. (2) , (3)
, (3)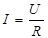 , (4)
, (4) , (5)
, (5) .
. , (6)
, (6) .
.


