Задачи для самоконтроля. 1. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределённый по площади заряд с поверхностной плотностью s1
1. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределённый по площади заряд с поверхностной плотностью s1 =1 нКл/м2 и s2 =3 нКл/м2. Определить напряжённость поля: а) между пластинами; б) вне пластин. Ответ: а) Е1 = 2. Плоская квадратная пластинка со стороной а =10 см находится на некотором расстоянии от бесконечной равномерно заряженной (s =1 мкКл/м2) плоскости. Плоскость пластины составляет угол b =30° с линиями поля. Найти поток yD электрического смещения через эту пластинку. Ответ: yD = 0, 5 s× а2sinb = 2, 5 нКл. 3. В поле, созданном заряженной сферой радиусом 10 см, движется электрон по радиусу между точками, находящимися на расстоянии 12 и 15 см от центра сферы. При этом скорость электрона изменяется от 2× 105 до 2× 106 м/с. Найти поверхностную плотность заряда сферы. Ответ: 4. Между пластинами плоского конденсатора помещено два слоя диэлектриков – слюдяная пластина (e1 =7) толщиной d1 =1 мм и парафин (e2 =2) толщиной d2 =0, 5 мм. Определить напряжённость электрических полей в слоях диэлектрика, если разность потенциалов между пластинами конденсатора U =500 В. Ответ: Е1 = 182 кВ/м; Е2 =637 кВ/м. 5. Некоторый заряд равномерно распределен внутри шара из диэлектрика. Во сколько раз энергия электростатического поля W1, локализованная в объеме шара, меньше энергии W2, локализованной вне шара? Диэлектрическая проницаемость e =1 и в диэлектрике, и в окружающем пространстве. Ответ: 4. 6. Напряженность электрического поля в проводнике, изготовленном из материала с удельным сопротивлением r, равна E. Длина проводника l, диаметр d. Этот проводник подсоединен к источнику питания с ЭДС, равной e. Найти ток в цепи и внутреннее сопротивление источника ЭДС. Ответ: I = 5. Падение напряжения в проводнике, состоящем из двух последовательно соединенных кусков медной и алюминиевой проволоки одинаковой длины (l 1 = l 2 = 10 м) и диаметра, равно 10 В. Найти удельную тепловую мощность тока в медной проволоке. Удельное сопротивление меди r1 = 17 нОм·м, алюминия - r2 = 25 нОм·м. Ответ: 6. Через диэлектрическую прокладку цилиндрического конденсатора, диэлектрическая проницаемость которой равна e, протекает ток. Считая, что удельное сопротивление прокладки равно r, найти, во сколько раз уменьшится заряд конденсатора за время t. Ответ:
|

 ; б) Е2 =
; б) Е2 = 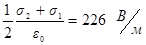 .
. нКл/м2 .
нКл/м2 . .
. ; r =
; r =  .
. = 0, 96× 10 7 Вт/м3 .
= 0, 96× 10 7 Вт/м3 . .
.


