Контрольное задание № 3
301. Две длинные одноимённо заряженные нити расположены на расстоянии r =10 см друг от друга. Линейная плотность заряда на нитях t1=t2 =10 мкКл/м. Найти модуль и направление вектора напряжённости 302. Два точечных заряда 6, 7 и 13, 2 нКл находятся на расстоянии 5 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3 см от первого заряда и 4 см - от второго. 303. Шарик, имеющий массу 0, 4 г и заряд 4, 9 нКл, подвешен на нити в поле плоского конденсатора, заряд которого 4, 43 нКл и площадь пластин 50 см2. На какой угол от вертикали отклонится при этом нить с шариком? 304. На отрезке тонкого прямого проводника длиной l =10 см равномерно распределён заряд с линейной плотностью t =0, 3 мкКл/м. Вычислить напряжённость, создаваемую этим зарядом в точке, расположенной на оси проводника и удалённой от ближайшего конца отрезка на расстояние, равное длине этого отрезка. 305. Диполь с электрическим моментом ре =10 -10 Кл× м подвешен на упругой нити. При возбуждении электрического поля напряженностью Е =3× 103 В/м перпендикулярно плечу диполя и нити диполь повернулся на угол a =30о. Определить постоянную кручения нити. Постоянной кручения называют величину, равную моменту силы, который вызывает закручивание нити на один радиан. 306. Определить напряженность и потенциал поля, создаваемого точечным диполем с электрическим моментом ре =4× 10 -12 Кл× м на расстоянии r =10 см от центра диполя, в направлении, составляющем угол j =60о с вектором электрического момента. 307. Тонкий стержень длиной 10 см равномерно заряжен с линейной плотностью t =1 мкКл/м. На продолжении оси стержня на расстоянии а =20 см от ближайшего его конца находится точечный заряд q =100 нКл. Определить силу взаимодействия заряженного стержня и точечного заряда. 308. Тонкое кольцо радиусом R =8 см равномерно заряжено с линейной плотностью t =10 нКл/м. Найти напряжённость электрического поля в точке, равноудалённой от всех точек кольца на расстояние r =10 см. 309. Металлический шар имеет заряд q1 =0, 1 мкКл. На расстоянии, равном радиусу шара, от его поверхности находится конец нити, вытянутой вдоль силовой линии. Нить несёт равномерно распределённый по длине заряд q2 =10 нКл. Длина нити равна радиусу шара. Определить силу, действующую на нить, если радиус шара R =10 см. 310. На оси равномерно заряженного кольца радиусом R =10 см расположен стержень длиной l =20 см. Стержень равномерно заряжен с линейной плотность заряда t =10 нКл/м. Заряд кольца равен 100 нКл. Ближайший конец стержня находится в центре кольца. Найти силу взаимодействия кольца и стержня. 311. Плоская круглая пластинка радиусом r =10 см находится в воде (e =81) на некотором расстоянии от бесконечной равномерно заряженной (s =2 мкКл/м2) плоскости. Плоскость пластины составляет угол b =30° с линиями поля. Найти поток вектора напряженности через эту пластинку. 312. Электрическое поле создано бесконечной, равномерно заряженной нитью (t =0, 3 мкКл/м). Определить поток вектора напряженности через прямоугольную площадку, две большие стороны которой параллельны нити и одинаково удалены от нее на расстояние r =20 см. Стороны площадки имеют размеры: а =20 см, b =40 см. 313. Металлический шар радиусом R =5 см несёт заряд q =1 нКл. Шар окружён слоем эбонита (e =2) толщиной d =2 см. Вычислить напряжённость электрического поля на расстоянии: а) r1 =3 см; б) r2 =6 см; в) r3 =9 см от центра шара. 314. Две металлические концентрические сферы имеют радиусы R1 =5 см и R2 =7 см. Заряд внутренней сферы q1 =-3, 2 нКл, внешней - q2 =8, 2 нКл. Найти напряжённость электрического поля на расстоянии: а) r1 =2 см; б) r2 =6 см; в) r3 =9 см от центра сфер. 315. Имеются две концентрические металлические сферы радиусами R1 =3 см и R2 =6 см. Пространство между сферами заполнено парафином (e =2). Заряд внутренней сферы q1 =-1 нКл, а внешней - q2 =2 нКл. Найти напряжённость электрического поля на расстоянии: а) r1 = 1 см; б) r2 = 5 см; в) r3 = 9 см от центра сфер. 316. На металлической сфере радиусом R =10 см находится заряд q =1 нКл. Определить напряжённость электрического поля в следующих точках: а) на расстоянии r1 =8 см от центра сферы; б) на её поверхности; в) на расстоянии r2 =15 см от центра сферы. 317. Большая плоская пластина из эбонита (e =2, 6) толщиной d =1 см несет заряд, равномерно распределенный по объему с плотностью r =100 нКл/м3. Найти напряженность электрического поля вблизи центральной части пластины, вне ее и на малом расстоянии от ее поверхности. 318. Металлический шар радиусом R1, несущий заряд q =1 нКл, окружен концентрическим полым металлическим шаром с внутренним радиусом R2 и внешним R3. Заряд внешнего шара равен нулю. Построить график зависимости напряженности поля от расстояния до центра шаров. Найти потенциал шаров, если в бесконечности потенциал равен нулю. 319. Длинная бесконечная тонкостенная металлическая трубка радиусом R =2 см несёт равномерно распределённый по поверхности заряд (s =1мкКл/м2).Определить напряжённость поля в точках, отстоящих от оси трубки на расстояниях r1 =1 см и r2 =3 см. 320. Прямой металлический стержень диаметром d =5 см и длиной l =4 м несёт равномерно распределённый по поверхности заряд q =500 нКл/м. Определить напряжённость поля в точке, находящейся против середины стержня на расстоянии 1 см от его поверхности. 321. Определить потенциал в центре кольца с внешним диаметром D =0, 8 м и внутренним диаметром d =0, 4 м, если на нём равномерно распределён заряд q =6× 10-7 Кл. 322. По тонкому кольцу радиусом R =10 см равномерно распределён заряд с линейной плотностью t =10 нКл/м. Построить график зависимости потенциала от расстояния до центра кольца и определить потенциал в точке, лежащей на оси кольца на расстоянии 5 см от центра. 323. Электрическое поле образовано положительно заряженной бесконечной нитью с линейной плотностью заряда в 2× 10 -9 Кл/см. Какую скорость получит электрон под действием поля, приблизившись к нити с расстояния в 1 см до расстояния 0, 5 см от нити? 324. Заряд распределён равномерно по бесконечной плоскости с поверхностной плотностью 10 нКл/м2. Определить разность потенциалов двух точек поля, одна их которых находится на плоскости, а другая удалена от плоскости на расстояние d =10 см. 325. Электрическое поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s =2 мкКл/м2. В этом поле вдоль прямой, составляющей угол a =60° с плоскостью, из точки 1 в точку 2, расстояние между которыми Dr =20 см, перемещается точечный электрический заряд q =10 нКл, удаляясь от плоскости. Определить работу сил поля по перемещению заряда (точка 1 расположена на произвольном расстоянии от плоскости). 326. Вдоль силовой линии однородного электрического поля движется протон. В точке поля с потенциалом j1 =100 В протон имел скорость u1 =0, 1 Мм/с. Определить потенциал j2 точки поля, в которой скорость протона возрастёт в n =2 раза. Отношение заряда протона к его массе q/m =96 МКл/кг. 327. Диполь с электрическим моментом ре =10-10 Кл м свободно устанавливается в однородном электрическом поле Е =1500 В/см. Вычислить работу, необходимую для того, чтобы повернуть диполь на угол j =180о. 328. Тонкий стержень длиной 10 см несёт равномерно распределённый заряд 1 нКл. Определить потенциал электрического поля в точке, лежащей на оси стержня на расстоянии 20 см от ближайшего его конца. 329. Бесконечно длинная прямая нить заряжена равномерно с линейной плотностью t =0, 40 мкКл/м. Вычислить разность потенциалов точек 1 и 2, если точка 2 находится дальше от нити, чем точка 1 в n =2 раза. 330. Бесконечно длинная прямая нить заряжена равномерно с линейной плотностью t =0, 01 мкКл/м. Вычислить разность потенциалов точек 1 и 2, удалённых от нити на расстояния r1 =2 см и r2 =4 см. 331. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0, 8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина e =1, 6. 332. Расстояние между обкладками плоского конденсатора составляет d =5 мм. После зарядки конденсатора до разности потенциалов U =500 В между обкладками вдвинули стеклянную пластину (e =7). Определить: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластине. 333. Расстояние между пластинами плоского конденсатора составляет d1 =1 см, разность потенциалов U =200 В. Определить поверхностную плотность связанных зарядов эбонитовой пластины (e =3) толщиной d2 =8 мм, помещённой на нижнюю пластину конденсатора. 334. Пространство между пластинами плоского конденсатора заполнено диэлектриком с диэлектрической восприимчивостью 0, 8. На пластины конденсатора подано напряжение 4 кВ. Найти поверхностную плотность зарядов на диэлектрике. Расстояние между пластинами равно 5 мм. 335. Диэлектрик поместили в электрическое поле напряжённостью Ео =20 кВ/м. Чему равна поляризованность Р диэлектрика, если напряжённость среднего макроскопического поля в диэлектрике оказалась равной 4 кВ/м? 336. У поверхности фарфоровой пластины (e =6) напряжённость поля в вакууме 200 В/см и образует с нормалью к поверхности угол 40°. Определить: 1) угол между направлением поля и нормалью к пластине внутри пластины; 2) напряжённость поля в фарфоре. 337. Во внешнем электрическом поле напряжённостью Ео =40 МВ/м поляризованность жидкого азота Р оказалась равной 109 мкКл/м2. Определить диэлектрическую проницаемость жидкого азота. 338. Одной из пластин плоского конденсатора площадью S =0, 2 м2 сообщили заряд q =10-9 Кл (другая пластина соединена с «землей»). Расстояние между пластинами d =2 мм. Между пластинами (параллельно им) находятся стеклянная (e =6) и эбонитовая (e =2, 6) пластинки, толщины которых равны соответственно d1 =0, 5 мм и d2 =1, 5мм. Определить напряженность электрического поля в стекле и эбоните, а также поверхностные плотности связанных зарядов на них. 339. В однородное электрическое поле с напряженностью E0 =100 В/м помещена пластина из однородного и изотропного диэлектрика с проницаемостью e =2. Пластина расположена перпендикулярно к 340. Плоский конденсатор заряжен до некоторой разности потенциалов. В конденсатор вдвинули диэлектрическую пластинку. После этого для восстановления прежней разности потенциалов пришлось увеличить заряд конденсатора в три раза. Найти диэлектрическую проницаемость пластинки. 341. Одинаковые заряды Q =100 нКл расположены в вершинах квадрата со стороной 10 см. Определить потенциальную энергию этой системы. 342. Площадь пластин плоского конденсатора 100 см2 и расстояние между ними 5 мм. Какая разность потенциалов была приложена к пластинам конденсатора, если известно, что при разряде конденсатора выделилось 4, 19× 10-3 Дж тепла? 343. Найти потенциальную энергию системы трех точечных зарядов: q1 =10 нКл, q2 =20 нКл, q3 =-30 нКл, расположенных в вершинах равностороннего треугольника со стороной 10 см. 344. Два конденсатора, ёмкости которых С1 =600 пФ и С2 =1000 пФ, соединили последовательно. Батарею заряжают до разности потенциалов U =20 кВ. Затем конденсаторы, не разряжая, соединяют параллельно. Определить энергию разряда, происходящего при этом переключении. 345. 64 капли ртути, каждая радиусом r =1 мм и с зарядом q =1 нКл, находятся на бесконечном расстоянии друг от друга, а затем сливаются в одну каплю. Определить изменение энергии системы при этом процессе. 346. Точечный заряд q =3, 0× 10-8 Кл помещается в центре шарового слоя из однородного изотропного диэлектрика с e =3. Внутренний радиус слоя 250 мм, внешний - 500 мм. Найти энергию W, заключенную в диэлектрике. 347. Заряженный шар А радиусом 2 см приводится в соприкосновение с незаряженным шаром В, радиус которого 3 см. После того как шары разъединили, энергия шара В оказалась равной 0, 4 Дж. Какой заряд был на шаре А до их соприкосновения? 348. Пластины плоского конденсатора площадью 100 см2 каждая притягиваются друг к другу с силой в 3× 10-2 Н. Пространство между пластинами заполнено слюдой (e =6). Найти энергию в единице объема поля. 349. Плоский воздушный конденсатор с площадью пластин 100 см2 и расстоянием между ними в 1 мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением отключается. 350. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом равна 2× 10-5 Дж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна 7× 10-5 Дж. Найти диэлектрическую проницаемость диэлектрика. 351. К источнику ЭДС, равной 3 В, имеющему внутреннее сопротивление 1 Ом, подключена внешняя цепь, состоящая из двух параллельно соединенных сопротивлений по 4 Ом каждое. Найти разность потенциалов между клеммами источника напряжения. 352. Источник с ЭДС e = 2, 0 В имеет внутреннее сопротивление r =0, 5 Ом. Определить падение напряжения внутри источника при токе в цепи I =0, 25 А. Найти внешнее сопротивление цепи при этих условиях. 353. Батарея гальванических элементов замкнута на внешнее сопротивление R1 =10 Ом и дает ток I1 =3 А. Если вместо сопротивления R1 включить сопротивление R2 =20 Ом, то ток I2 станет равным 1, 6 А. Найти ЭДС и внутреннее сопротивление батареи. 354. Какова электродвижущая сила элемента, если при измерении напряжения на его зажимах вольтметром, внутреннее сопротивление которого 20 Ом, получают напряжение UV =1, 37 В, а при замыкании элемента на сопротивление R =10 Ом в цепи возникает ток I =0, 132 А? 355. В цепь, состоящую из батареи и резистора сопротивлением R =8 Ом, включают вольтметр, сопротивление которого RV =800 Ом, один раз последовательно резистору, второй – параллельно. Определить внутреннее сопротивление батареи, если показания вольтметра в обоих случаях одинаковы. 356. Источник ЭДС замыкается двумя последовательно соединенными сопротивлениями R1 и R2. Если вольтметр подключить к сопротивлению R1, то он покажет 6 В, если к R2 - 4 В, если вольтметр подключить к источнику, то он покажет 12 В. Найти действительные значения напряжений на сопротивлениях R1 и R2. Внутренним сопротивлением источника пренебречь. 357. Определить удельное сопротивление проводника длиной l =2 м, если при плотности тока j =106 А/м2 на его концах поддерживается разность потенциалов U =2 В. 358. Из медной проволоки длиной l =120 м и площадью поперечного сечения S =24 мм2 намотана катушка. Найти приращение сопротивления катушки при нагревании ее от t1 =20 оC до t2 =70 оC. Удельное сопротивление меди r =17 нОм·м; температурный коэффициент сопротивления a =0, 0043 C-1. 359. Лампа накаливания потребляет ток, равный 0, 6 А. Температура вольфрамовой нити диаметром 0, 1 мм равна 2200 оC. Ток подводится медным проводом сечением S =6 мм2. Определить напряженность электрического поля: 1) в вольфраме (удельное сопротивление при 0 оC r =55 нОм·м; температурный коэффициент сопротивления a =0, 0045 oC-1); 2) в меди (температура подводящих проводов 20 оC). 360. Определить температурный коэффициент провода, составленного из алюминиевой проволоки сопротивлением 3 Ом (температурный коэффициент сопротивления a1 =0, 0045 oC-1) и железной проволоки сопротивлением 2 Ом (температурный коэффициент сопротивления a2 =0, 006 oC-1), соединенных последовательно. 361. Какая мощность выделяется в единице объема медного проводника длиной l =0, 2 м, если на его концах поддерживается разность потенциалов U =4 В? 362. Проводник, состоящий из двух последовательно соединенных кусков медной проволоки одинаковой длины (l 1= l 2=10 м), но разного диаметра (d1=2d2), подключили к источнику ЭДС. По проводнику протекает ток 1 А, при этом в первом куске в виде тепла за две секунды выделилось 10 Дж. Найти удельную тепловую мощность тока в обоих кусках проволоки. Удельное сопротивление меди r =17 нОм·м. 363. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока I1 =4 А развивается мощность P1 =10 Вт, а при силе тока I2 =6 А - мощность P2 =12 Вт. 364. От источника, на клеммах которого разность потенциалов U =50 кВ, требуется передать мощность N =5·103 кВт на расстояние l =5 км. Допустимая «потеря» напряжения в проводах n =1 %. Найти минимальный диаметр медного провода, пригодного для данной цели. 365. Какое время требуется для нагревания 2 л воды (с =4, 19× 103 Дж/кг× К) от 20 оС до кипения в электрическом чайнике, если напряжение в сети 220 В, сопротивление спирали чайника 20 Ом, а КПД чайника 70 %? 366. Спираль электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через t1 =10 мин, если другая, то через t2 =20 мин. Через сколько минут закипит вода, если обе секции включить: а) последовательно; б) параллельно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми. 367. При включении в сеть электроплитки с номинальной мощностью P0 =800 Вт разность потенциалов на клеммах розетки уменьшилась, а фактическая мощность электроплитки P1 стала равной 661 Вт. Какова мощность двух таких плиток, включенных параллельно в розетку? Изменением сопротивления плиток при изменении их накала пренебречь. 368. При каком сопротивлении внешней цепи источник с ЭДС e =10 В и внутренним сопротивлением r =20 Ом будет отдавать максимальную мощность? Какова величина этой мощности? 369. Электродвижущая сила батареи e =12 В. Наибольшая сила тока, которую может дать батарея, Imax =5 А. Какая наибольшая мощность может выделиться на подключенном к батарее резисторе с переменным сопротивлением? 370. Какое наименьшее число N одинаковых источников питания с ЭДС e =1 В и внутренним сопротивлением r =1 Ом необходимо взять, чтобы на внешнем сопротивлении R =10 Ом выделилась максимальная мощность? Максимальная сила тока Imax =2 А. 371. Какой заряд пройдет по проводнику, если в течение 10 с сила тока уменьшилась от Iо =10 А до 5 А? Считать, что сила тока уменьшается равномерно. 372. Какой заряд пройдет по проводнику, если в течение t =10 с сопротивление проводника равномерно возрастало, ток уменьшался от I1 =10 А до I2 =5 А, а разность потенциалов на концах проводника поддерживалась постоянной? 373. Сила тока в проводнике сопротивлением R =120 Ом равномерно возрастает от Iо =0 до Imax =5 А за время t =15 с. Определить выделившееся за это время в проводнике количество тепла. 374. По проводнику сопротивлением R =3 Ом течет равномерно нарастающий ток. Количество тепла, выделившегося за время t =8 с, равно Q =200 Дж. Определить заряд, прошедший за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю. 375. Ток в проводнике сопротивлением R =15Ом равномерно возрастает от Iо =0 до некоторого максимального значения в течение времени t =5 с. За это время в проводнике выделилась в виде тепла энергия Q =10 кДж. Найти среднее значение силы тока в проводнике за этот промежуток времени. 376. На рис. 1 сопротивление каждого проводника, включенного между двумя узлами, равно 1 Ом. Найти сопротивление цепи. 377. Найти сопротивление цепи, изображенной на рис. 2. Считать, что сопротивление каждого проводника, включенного между узлами, равно 1 Ом. 378. 379. Сопротивление каждого проводника, составляющего ребро куба, равно 10 Ом. Найти тепло, которое будет выделяться в этом кубе за одну секунду, если между точками A и C (рис. 3) этого куба поддерживается разность потенциалов U =10 В. 380. Определить ток, который будет протекать по проводам, подсоединенным к вершинам Bи Cкуба (рис. 3), составленного из сопротивлений величиной в 1 Ом, если он подключен к источнику тока с разностью потенциалов на выводах U =10 В.
Варианты контрольного задания № 3
|

 результирующего электрического поля в точке, находящейся на расстоянии а =10 см от каждой нити.
результирующего электрического поля в точке, находящейся на расстоянии а =10 см от каждой нити. . Определить электрическое смещение D и поляризованность диэлектрика P.
. Определить электрическое смещение D и поляризованность диэлектрика P.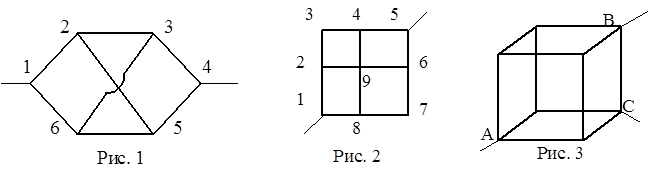 Сопротивление каждого проводника, составляющего ребро куба, равно 10 Ом (рис. 3). Найти тепло, которое будет выделяться в этом кубе за одну секунду, если между точками A и B этого куба поддерживается разность потенциалов U =10 В.
Сопротивление каждого проводника, составляющего ребро куба, равно 10 Ом (рис. 3). Найти тепло, которое будет выделяться в этом кубе за одну секунду, если между точками A и B этого куба поддерживается разность потенциалов U =10 В.


