Циркуляция магнитного поля (закон полного тока) в вакууме. Теорема Гаусса для магнитного поля
Теорема о циркуляции для магнитного поля в вакууме Циркуляция вектора магнитной индукции поля в вакууме равна алгебраической сумме токов, охватываемых этим контуром (т. е. результирующему току через поверхность, опирающуюся на контур L), умноженной на магнитную постоянную:
Силовые поля, для которых циркуляция силового вектора отлична от нуля, называются вихревыми или соленоидальными. Магнитное поле является вихревым, а его силовые линии (линии вектора Используя теорему о циркуляции, можно рассчитывать магнитные поля токов, обладающие определенной симметрией, например, индукции магнитных полей внутри тороида и бесконечно длинного соленоида. Для соленоида: В = m0·nI; для тороида: где n - число витков на единицу длины соленоида; N - полное число витков тороида; r - радиус окружности, лежащей внутри тороида; R1 и R2 - внутренний и наружный радиусы тороида.
Элементарным потоком магнитной индукции(магнитнымпотоком)сквозь малую поверхность площадью dS называется физическая величина, равная
Магнитный поток сквозь произвольную поверхность S (рис. 2.11)
Если магнитное поле однородное, а поверхность S плоская, то
Ф m=Вn× S = B× S cos(
Единица измерения магнитного потока в СИ - 1 Вб (вебер). Теорема Гаусса для магнитного поля (силовые линии поля замкнуты)
Магнитный поток сквозь произвольную замкнутую поверхность равен нулю:
|
.
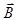) - замкнуты.
; R2< r < R1,
.
.
).
.
