Закон Био и Савара. Принцип суперпозиции. Магнитное поле прямого и кругового токов
где mо =4p× 10-7 Гн/м - магнитная постоянная, Принцип суперпозиции Магнитная индукция поля произвольной системы проводников с токами (или системы движущихся электрически заряженных частиц) равна геометрической сумме магнитных индукций полей всех малых элементов тока этих проводников (магнитных индукций полей всех движущихся зарядов), создаваемых в данной точке:
Закон Био и Савара в дифференциальной форме определяет индукцию магнитного поля, создаваемую линейным элементом тока:
где j - угол между элементом тока и вектором Согласно принципу суперпозиции магнитная индукция проводника с током I
Магнитное поле прямолинейного проводника MN с током I (рис. 2.5)
Если проводник бесконечно длинный, то j1 = 0, j2 = p. В = m0I/(2pr).
Магнитный момент контура с током(рис. 2.6)
где I – сила тока, S – площадь контура, Индукция магнитного поля кругового тока I радиусом R в произвольной точке А на оси кругового тока (рис. 2.7)
Индукция магнитного поля в центре кругового витка с током
Магнитное поле на оси короткого соленоида (рис. 2.8). Соленоидомназывается цилиндрическая катушка с током, состоящая из большого числа витков проволоки, которые образуют винтовую линию. Магнитная индукция на оси соленоида находится по формуле
где n - количество витков на единицу длины соленоида.
|

 Каждый движущийся электрический заряд создает в окружающем пространстве магнитное поле, индукция которого определяется выражением:
Каждый движущийся электрический заряд создает в окружающем пространстве магнитное поле, индукция которого определяется выражением: ;
;  ,
,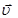 - скорость движения заряда,
- скорость движения заряда,  - радиус-вектор точки, где определяется индукция магнитного поля (рис. 2.3).
- радиус-вектор точки, где определяется индукция магнитного поля (рис. 2.3). ,
,  .
. ;
;  ,
,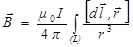 ,
,  .
. .
.
 , pm = I S,
, pm = I S, - вектор нормали к плоскости контура. Направление магнитного момента связано с направлением тока правилом правого винта.
- вектор нормали к плоскости контура. Направление магнитного момента связано с направлением тока правилом правого винта. ;
; .
. и
и  .
.
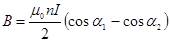 ,
,


