Применение уравнения Шредингера
а) Частица в бесконечно глубокой одномерной потенциальной яме Предположим, что частица может двигаться только вдоль оси х и ее движение ограничено непроницаемыми стенками в точках х = 0 и х = l. Зависимость потенциальной энергии от координат имеет в этом случае следующий вид (рис. 3):
Поскольку волновая функция в данном случае зависит только от координаты х, уравнение Шредингера упрощается следующим образом:
Решая уравнение (6.33) с использованием стандартных условий, можно получить собственные значения энергии частицы:
Энергетический спектр, как следует из (34), является дискретным. При этом расстояние между соседними энергетическими уровнями не является постоянным, а увеличивается с увеличением номера энергетического уровня. Нормированные собственные функции частицы в этом случае имеют вид
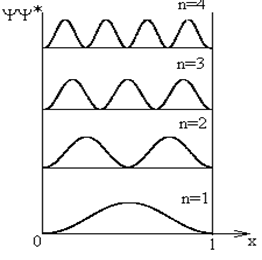
Графики этих функций показаны на рис. 4. На рис. 5 дана зависимость плотности вероятности обнаружения частицы от координаты x на различных расстояниях от стенок ямы, равная Y× Y*.
б) Прохождение частиц через потенциальный барьер
Пусть частица с энергией Е, движущаяся слева направо вдоль оси х, встречает на своем пути потенциальный барьер высотой U0 и шириной l (рис. 6). Из решения уравнения Шредингера в этом случае вытекает, что, во-первых, даже при Е> U0 имеется отличная от нуля вероятность того, что частица отразится от барьера. Во-вторых, при Е< U0 имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области, где х > l. Вероятность прохождения частицы через барьер может быть названа коэффициентом прозрачности D. Расчеты показывают, что в данном случае
Для потенциального барьера произвольной формы (рис. 7) формула (36) должна быть заменена более общей формулой
где U = U(x).
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере (рис. 7), в связи с чем это явление называют туннельным эффектом.
|



 (32)
(32) . (33)
. (33)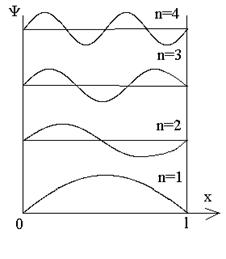
 (34)
(34)




 . (36)
. (36)
 , (37)
, (37)


