Статический расчет рамы
Расчетная схема рамы дана на рис. 56. Ввиду ломаного очертания ригеля и переменности его сечения приведенную изгибную жесткость сечения ригеля, нормального к его продольной оси, подсчитываем по формуле EI пр = EI максcos2θ k, где I макс - момент инерции сечения ригеля в середине пролета; θ - угол наклона нейтральной оси ригеля; k = 0, 15 + 0, 85β - коэффициент по СНиП II-25-80, прил. 4, табл. 3. В результате статического расчета рамы методом сил получены следующие формулы для определения опорных реакций и изгибающих моментов в опорных сечениях и коньке рамы (см. рис. 56): от равномерно распределенной нагрузки по ригелю VА = V Д = ql /2; VА = U Д = 5 qS 2/cos2θ k с/[8(H 2 k + f 2 k с)]; MА = M Д = 5 qS 2 Hf cos2θ k с/[8(H 2 k + f 2 k с); ME = ql 2/8 - 5 qS 2 f 2cos2θ k с/[8(H 2 k + f 2 k с)], где k с = EkIkS /(EI пр H); от ветровых нагрузок P 1 b, P 2 b , P 3 b, (ветер слева направо): VА = V Д = P 3 b //(2cos θ); U А = P 1 b H - (P 1 b - P 2 b ) H 3 k /[8(H 2 k + f 2 k с)] + 5 P 3 b S 2 f cos θ k с/[8(H 2 k + f 2 k с)]; U Д = P 2 b H + (P 1 b - P 2 b ) H 3 k /[8(H 2 k + f 2 k с)] - 5 P 3 b S 2 f cos θ k с/[8(H 2 k + f 2 k с)]; M А = P 1 b H 2/2 - (P 1 b - P 2 b ) H 4 k /[8(H 2 k + f 2 k с) + 5 P 3 b S 2 fH cos θ k с/[8(H 2 k + f 2 k с)]; M Д = P 2 b H 2/2 + (P 1 b - P 2 b ) H 4 k /[8(H 2 k + f 2 k с) - 5 P 3 b S 2 fH cos θ k с/[8(H 2 k + f 2 k с)]; M Е = P 3 b l 2/8 + (P 1 b - P 2 b ) H 3 fk /[8(H 2 k + f 2 k с) - 5 P 3 b S 2 fH cos θ k с/[8(H 2 k + f 2 k с)].
Рис. 56. Расчетная схема рамы и эпюры изгибающих моментов Определяем усилия в сечениях стойки 0 ≤ y ≤ H, считая расположение начала координат на уровне низа стойки, от: равномерно распределенной нагрузки M = MА - VАy; Q = UА; N = VА; ветровых нагрузок P 1 b, P 2 b, P 3 b: ветер слева направо M = M А - U А y + P 1 by 2/2; Q = U А - P 1 by; N = V А, ветер справа налево M = M Д- U Д y + P 2 b y 2/2; Q = U Д - R 2 b y; N = V Д. Определяем усилия в сечениях ригеля 0 ≤ x ≤ l /2, считая расположение начала координат на левой опоре от: равномерно распределенной нагрузки: M = V А x - qx 2/2 - 2 U А fx / l; Q = (V А- qx)cosθ - U Аsinθ; N = (V А - qx)sinθ + U Аcosθ; ветровых нагрузок P 1 b, P 2 b, P 3 b: M = V А x - Р 3 bx 2/2 cos θ - 2 fx (U А - P 1 bH)/ l; Q = (V А - P 3 bx /cos θ)cos θ - (U А - P 1 b Н)sin θ; N = (V А - P 3 bx /cos θ)sin θ + (U А - P 1 b H)cos θ. Положение расчетного сечения x в двускатном ригеле определяем по формуле x = lh 0/(2 h 1) = 17, 64× 0, 581/(2× 1, 022) = 5 м. По вышеприведенным формулам были подсчитаны усилия в сечениях рамы и представлены в табл. 35. Эпюры изгибающих моментов представлены на рис. 56. Расчетные величины усилий определяем при следующих основных сочетаниях нагрузок: собственный вес и снеговая нагрузка; собственный вес, снеговая и ветровая нагрузки с учетом коэффициента сочетаний n с = 0, 9. Для наиболее невыгодных сочетаний нагрузок производим проверку предварительно назначенных сечений элементов рамы по соответствующим формулам и указаниям СНиП II-25-80. Таблица 35
РАСЧЕТ СТОЙКИ Наиболее напряженным является сечение, защемленное в фундаменте. Усилия в этом сечении равны: M = 22, 62 кН× м; Q = 5, 16 кН; N = 55, 8 кН. Геометрические характеристики расчетного сечения b = 140 мм; h = 363 мм; F расч = F бр = 140× 363 = 5, 08× 104 мм2; W бр = W расч = 140× 3632/6 = 3, 07× 106 мм3; l 0 = μ l = 2, 2× 5, 45 = 12 м. Для стойки принимаем пиломатериал 3-го сорта. Тогда согласно СНиП II-25-80, табл. 3. R и = R с = R см= 11× m и/γ n = 11× 1, 2/0, 95 = 13, 9 МПа. Определяем φ = 3000/λ 2 = 3000/114, 42 = 0, 229; ξ = 1 - N /(φ R с F бр) = 1 - 55, 8× 103/(0, 229× 13, 9× 5, 08× 104) = 0, 655; K и = α и + ξ (1 - α и) = 1, 22 + 0, 655(1 - 1, 22) = 1, 08; M д = M /(ξ K и) = 22, 62/(0, 655× 1, 08) = 31, 98 кН× м. Проверяем прочность сжато-изгибаемой стойки N / F расч + M Д/ W расч = 55, 8× 103/5, 08× 104 + 31, 98× 106/3, 07× 106 = 11, 5 < R с = 13, 9 МПа.
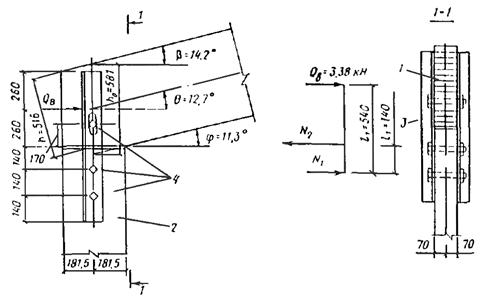
Рис. 57. Карнизный узел рамы 1 - гнутоклееный ригель; 2 - стойка; 3 - уголки 63 ´ 63 ´ 5; 4 - болты М20 Расчет ригеля Для опорного сечения: Q макс = 54, 3 кН; h = (h 0 - hk tg φ /2)cos φ = (581 - 363× 0, 1998/2)0, 9755 = 531 мм; b = 140 мм. Максимальные скалывающие напряжения τ = 3 Q макс/(2 bh) = 3× 54, 3× 103/(2× 140× 531) = 1, 09 < R ск/γ n = 1, 5/0, 95 = 1, 58 МПа. Требуемая длина опорной площадки из условия смятия древесины равна: l см = Q максγ n /(bR см α ) = 54, 3× 103× 0, 95/(140× 3, 2) = 116 мм, где R см α = R см/[1 + (R см/ R см90 - 1)sin3 α ] = 15/[1 + (15/3 - 1)0, 97553] = 3, 2 МПа; α = 90° - θ = 90° - 12, 7° = 77, 3°. Длину опорной площадки принимаем 363 мм (рис. 57). Для расчетного сечения по изгибу x = 5010 мм: Mx = 198, 38 кН× м; Qx = 23, 92 кН; Nx =-8, 45 кН. Сечение находится вне криволинейной зоны. Геометрические характеристики сечения: hx = [ h 0 + x (tg γ - tg φ)]cos θ = (581 + 5000× 0, 05)0, 9755 = 811 мм. F расч = 140× 811 = 11, 35× 104 мм2; W расч = W бр = 140× 8112/6 = 15, 35× 106 мм3. Определяем: λ = l р/(0, 289 h) = 17640/(0, 289× 1200) = 51; φ = 3000/λ 2 = 3000/512 = 1, 16; К ж N = 0, 07 + 0, 93 h 0/ h = 0, 07 + 0, 93× 581/1200 = 0, 52; R и = R с = R см = 15 m б/γ n = 15× 0, 9/0, 95 = 14, 2 МПа; m б = 0, 9 для расчетного сечения с hx = 811 мм; ξ = 1 - N /(φ R с F брКж N) = 1 - 8, 45× 103/(1, 16× 14, 2× 140× 1200× 0, 52) = 0, 99; M д = M /ξ = 198, 38/0, 99 = 200, 2 кН× м; N / F расч + M д/ W расч = 8, 45× 103/11, 35× 104 + 200, 2× 106/15, 35× 106 = 13, 1 < R с= 14, 2 МПа. Сжатая кромка ригеля раскреплена из плоскости изгиба прогонами кровли с шагом 2× 1, 5 = 3 м, т.е. l р = 3 < 140 b 2/(m б h) = 140× 0, 142/(0, 9× 0, 811) = 3, 6 м. Поэтому проверка устойчивости плоской формы деформирования не требуется. Проверяем радиальные растягивающие напряжения в середине пролета K и рад M д/ W расч = 246× 106× 0, 045/33, 6× 106 = 0, 33 ≈ R р90/0, 95 = 0, 3/0, 95 = 0, 32 МПа, где M д = M /ξ = 243, 9/0, 99 = 246 кН× м; W расч = bh 2/6= 140× 12002/6 = 33, 6× 106 мм3; K и рад - коэффициент, определяемый по графику рис. 29 при φ = 14° и h / r = 0, 125; r = r 0 + h /2 = 9, 01 + 1, 2/2 = 9, 61 м.
|