Типы связей между функциями
Одним из важных моментов при проектировании ИС с помощью методологии SADT является точная согласованность типов связей между функциями. Диаграмму SADT уровня ниже контекстной теоретически можно было бы нарисовать на одном листе огромного размера, разместив на нем все функции, число которых может достигать сотен-тысяч и более. Поскольку это не удобно, рисуют иерархию диаграмм декомпозиции, каждая из которых содержит до 10 блоков (рекомендуется 4-6 блоков на одной диаграмме). Разделить общую гипотетическую диаграмму на диаграммы декомпозиции можно разными путями. Общий принцип деления состоит в том, чтобы блоки с большей степенью связности (значимости, ранга) были размещены на одном листе диаграммы декомпозиции, а блоки с низкой значимостью связности – на разных листах диаграммы. Если блоки размещены на одном листе диаграммы – между ними есть связность (а иначе, зачем мы их вместе поместили?). Различают, по крайней мере, семь типов связывания (табл. 5.1).
Таблица 5.1 - Типы связывания функциональных блоков
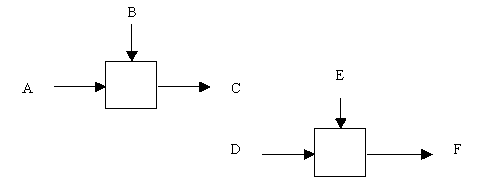
Ниже каждый тип связи кратко определен и проиллюстрирован с помощью типичного примера из SADT. (0) Тип случайной связности: наименее желательный. Случайная связность возникает, когда конкретная связь между функциями мала или полностью отсутствует. Это относится к ситуации, когда имена данных на SADT-дугах в одной диаграмме не имеют связи друг с другом. Крайний вариант этого случая показан на рисунке 5.8.
Рис. 5.8 - Случайная связность
(1) Тип логической связности. Логическое связывание происходит тогда, когда данные и функции собираются вместе вследствие того, что они попадают в общий класс или набор элементов, но необходимых функциональных отношений между ними не обнаруживается. Рисунок аналогичен рис. 5.8.
(2) Тип временной связности. Связанные по времени элементы возникают вследствие того, что они представляют функции, связанные во времени, когда данные используются одновременно или функции включаются параллельно, а не последовательно. Рисунок аналогичен рис. 5.8. (3) Тип процедурной связности. Процедурно-связанные элементы появляются сгруппированными вместе вследствие того, что они выполняются в течение одной и той же части цикла или процесса. Пример процедурно-связанной диаграммы приведен на рисунке 5.9.
Рис.5.9 - Процедурная связность
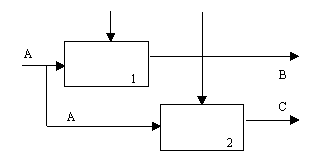
(4) Тип коммуникационной связности. Диаграммы демонстрируют коммуникационные связи, когда блоки группируются вследствие того, что они используют одни и те же входные данные и/или производят одни и те же выходные данные (рисунок 5.10).
Рис. 5.10 - Коммуникационная связность
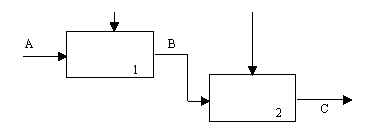
(5) Тип последовательной связности. На диаграммах, имеющих последовательные связи, выход одной функции служит входными данными для следующей функции. Связь между элементами на диаграмме является более тесной, чем на рассмотренных выше уровнях связок, поскольку моделируются причинно-следственные зависимости (рисунок 5.11).
Рис. 5.11 - Последовательная связность
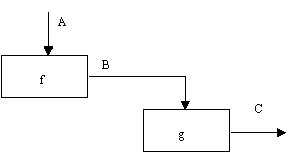
(6) Тип функциональной связности. Диаграмма отражает полную функциональную связность, при наличии полной зависимости одной функции от другой. Диаграмма, которая является чисто функциональной, не содержит чужеродных элементов, относящихся к последовательному или более слабому типу связности. Одним из способов определения функционально-связанных диаграмм является рассмотрение двух блоков, связанных через управляющие дуги, как показано на рисунке 5.12.
Рис. 5.12 - Функциональная связность
В математических терминах необходимое условие для простейшего типа функциональной связности, показанной на рисунке 5.12, имеет следующий вид:
C = g(B) = g(f(A))
Ниже в таблице представлены все типы связей, рассмотренные выше. Важно отметить, что уровни 4-6 устанавливают типы связностей, которые разработчики считают важнейшими для получения диаграмм хорошего качества.
Таблица 5.2 – Значимость типов связности
|