Упражнения.
Задачи
7.2.4 Построить проекции D1E1, D2E2 отрезка DE, определяющего расстояние между параллельными плоскостями S(ABC) и Q(mXn). Определить угол наклона S и Q к плоскости проекций П1.
Примеры решения задач: Задача 1 Отрезок прямой общего положения АВ преобразовать в горизонтально проецирующую прямую. Решить способом замены плоскостей проекций. Решение. На первом этапе заменим фронтальную плоскость П 2 проекций на новую П 4 так, чтобы прямая (АВ) стала фронталью. Поэтому выбираем х 1║ (A1B1). Ось проекций х старой системы выбираем так, чтобы было меньше дополнительных построений. Строим новую фронтальную проекцию (А4 В4) прямой линии. Решена первая задача.
На втором этапе решения новую горизонтальную плоскость П5 выбираем так, чтобы прямая линия (АВ) стала горизонтально проецирующей. У такой прямой ось х4, 5 проекций должна быть перпендикулярна фронтальной проекции (А 4В 4). По линии связи откладываем координату у заменяемой проекции и получаем А5 =В5 - горизонтальную проекцию горизонтально проецирующей прямой (АВ).
Задача 2 Плоскость Σ общего положения преобразовать в горизонтальную плоскость уровня. Решить способом замены плоскостей проекций. Решение. На первом этапе ее решения заменим фронтальную плоскость П2 проекций на новую П4 так, чтобы плоскость Σ стала фронтально проецирующей. Для этого в плоскости Σ построим произвольную горизонталь На втором этапе заменяем горизонтальную проекцию. Выбираем новую ось х4, 5 так, чтобы она совпала с фронтальной проекцией Σ 4 плоскости Σ . Строим новую горизонтальную проекцию, откладывая по линиям связи координаты: Задача 3 Отрезок прямой общего положения АВ преобразовать в горизонтально проецирующую прямую. Решить способом плоскопараллельного перемещения. Решение. При плоскопараллельном перемещении объекта [AB] относительно горизонтальной плоскости проекций все его точки (А и В) движутся в горизонтальных плоскостях уровня. Это значит, что отрезок [AB] может перемещаться в любое положение, но фронтальные проекции А2 и В2 его концов могут перемещаться только по проекциям горизонтальных плоскостей уровня., линии которых одновременно служат горизонтальными линиями связи. Заметим, что, выбирая положение свободно перемещаемой проекции, мы сможем сближать или раздвигать новые проекции и изображать их справа или слева от старых проекций на любом удалении. На первом этапе прямую линию [AB] мы переместили до положения
Задача 4 Плоскость Γ общего положения преобразовать в горизонтальную плоскость уровня. Решить способом плоскопараллельного перемещения. Решение. Построим в плоскости (АВС) горизонталь
Проводим прямую Горизонтальная проекция
|



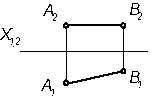







 и выберем старую ось х1, 2 проекций. В примере ось х1, 2 выбрана произвольно, но можно ее выбрать, например, совпадающей с h2 . строим
и выберем старую ось х1, 2 проекций. В примере ось х1, 2 выбрана произвольно, но можно ее выбрать, например, совпадающей с h2 . строим  , тогда прямая h(h1 h4) в системе
, тогда прямая h(h1 h4) в системе  становится фронтально проецирующей и плоскость Σ (h, С) тоже стала фронтально проецирующей.
становится фронтально проецирующей и плоскость Σ (h, С) тоже стала фронтально проецирующей.
 Проводим прямые а5 и b5.. плоскость Σ стала горизонтальной плоскостью уровня
Проводим прямые а5 и b5.. плоскость Σ стала горизонтальной плоскостью уровня фронтали, где
фронтали, где 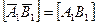 , а затем до положения
, а затем до положения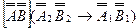 горизонтально проецирующей прямой, где
горизонтально проецирующей прямой, где 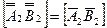 и
и  или
или  ║
║  . Выбирая положения
. Выбирая положения  и
и 
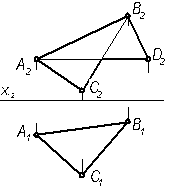
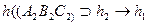 и перемесим треугольник относительно горизонтальной плоскости проекций так, чтобы прямая стала фронтально проецирующей прямой. Для этого строим в выбранном месте прямую
и перемесим треугольник относительно горизонтальной плоскости проекций так, чтобы прямая стала фронтально проецирующей прямой. Для этого строим в выбранном месте прямую  и в любом месте отмечаем точку, например
и в любом месте отмечаем точку, например  , от которой откладываем отрезок
, от которой откладываем отрезок  . На этом отрезке строим
. На этом отрезке строим  так, чтобы обход вершин обоих треугольников выполнялся в одном направлении. Проводим дуги окружностей из точки
так, чтобы обход вершин обоих треугольников выполнялся в одном направлении. Проводим дуги окружностей из точки  , а из точки
, а из точки  радиусом
радиусом  и в пересечении построенных дуг отмечаем точку
и в пересечении построенных дуг отмечаем точку  с учетом направления обхода вершин.
с учетом направления обхода вершин.
 и на ней откладываем отрезок
и на ней откладываем отрезок  . Соединяем вершину
. Соединяем вершину  и
и  и
и 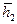 . Фигура стала фронтально проецирующей. Перемещая фигуру относительно фронтальной плоскости проекций до положения
. Фигура стала фронтально проецирующей. Перемещая фигуру относительно фронтальной плоскости проекций до положения 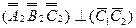 , мы преобразуем заданную плоскость в горизонтальную плоскость уровня.
, мы преобразуем заданную плоскость в горизонтальную плоскость уровня. определится в пересечении линий связи и
определится в пересечении линий связи и  . Возвращение к старым проекциям производится в обратном порядке.
. Возвращение к старым проекциям производится в обратном порядке.


