Решение дифференциальных уравнений и систем
Нелинейные дифференциальные уравнения и системы с такими уравнениями, как правило, не имеют аналитических методов решения, и здесь особенно важна возможность из решения численными методами. В большинстве случаев желательно представление решений в графическом виде, что также позволяет MathCad. Для решения задач такого класса можно использовать ряд функций: Odesolve(x, b, [step]) - возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given. x - переменная интегрирования, действительное число b - конечная точка отрезка интегрирования step - величина шага по переменной интегрирования (необязательный аргумент) Rkadapt(y, x1, x2, n, F) - возвращает матрицу решений методом Рунге-Кутта с переменным шагом для системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F, на интервале от x1 до x2 при фиксированном числе шагов n; rkfixed(y, x1, x2, n, F) - возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F, на интервале от x1 до x2 при фиксированном числе шагов n. Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и является его заключительным ключевым словом. Пример использования функции приведен на рис.68.
Рис.68. Пример решения дифференциального уравнения второго порядка с помощью функции Odesolve.
Системы линейных дифференциальных уравнений первого порядка решаются с помощью функции Rkfixed. На рис.2 приведен пример применения функции rkfixed для решения дифференциального уравнения, описывающего процесс свободных затухающих колебаний величины электрического заряда q (К) на конденсаторе с емкостью С (Ф), включенного в замкнутый контур, содержащий также сопротивление R (Ом) и индуктивность L (Гн). Этот процесс описывается дифференциальным уравнением второго порядка
где
b – коэффициент затухания, 1/с, wc– круговая частота собственных колебаний контура, 1/с, Исходные данные к решению задачи: Начальное условие: t=0, Vq=0, q=q0.
Процесс затухания колебаний рассчитать до tk Исходное дифференциальное уравнение второго порядка может быть преобразовано в систему дифференциальных уравнений первого порядка. Для этого введем подстановки: q0=q q1= Дифференциальное уравнение второго порядка преобразуем в систему дифференциальных уравнений первого порядка:
Правые части системы дифференциальных уравнений записываются в вектор правых частей системы уравнений D(t, q). Матрица Z размерности n строк по числу точек вывода результатов решения и m+1 столбцов, равным числу уравнений в системе. В столбцах матрицы содержатся значения переменных соответственно t,
Рис.69. Пример решения дифференциального уравнения второго порядка с помощью функции rkfixed.
|




 =d2q/dt2 – ускорение изменения заряда, К/с2;
=d2q/dt2 – ускорение изменения заряда, К/с2; =dq/dt – скорость изменения заряда, К/с;
=dq/dt – скорость изменения заряда, К/с;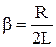 ;
;
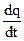

 ,
,  . На рис.2 представлен график изменения заряда от времени.
. На рис.2 представлен график изменения заряда от времени.



