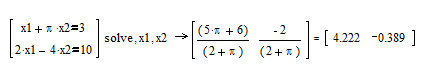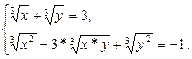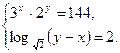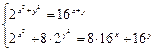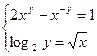Функция
Solve, x1, х2...х3
позволяет найти значение перечисленных переменных, при которых содержащее их выражение становится равным нулю. Для решения системы уравнений в шаблон функции solve вставляется вектор, длина которого равна количеству уравнений в системе. Уравнения записываются в вектор.
На рис. 68 приведен пример применения функции solve для решения систем уравнений.

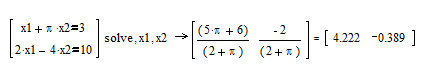
Рис.68. Пример применения функции solve для решения систем уравнений.
Оборудование, инструменты и приборы
ПЭВМ, система MathCad
Варианты заданий
Варианты заданий приведены в таблицах 4.12 -4.15.
Задание 1
Решить уравнение согласно заданию своего варианта. Найти все корни уравнения. Точность решения 0.0001. Варианты заданий приведены в табл.4.12.
Таблица 4.12
Варианты заданий
| № вар
| Задание
| № вар
| Задание
| № вар
| Задание
|
|
| 1/2*x2+3*cos(x)– 5=0
|
| 
|
| 2*x2+ln(2*x–x2) =0
|
|
| 
|
| ln(2*x–x3)+2=0
|
| 4*x2–5*x-1–2=0
|
|
| sin(x)–5*x3+1=0
|
| 
|
| x3–8*x2+1.5=0
|
|
| |x|–3*x2+1=0
|
| 4*|sin(x)|+x2–4=0
|
| 4*cos(x)+x2–4=0
|
|
| 
|
| 7*|sin(x)|–x–5=0
|
| 1/2*x3+3*cos(x)+2=0
|
|
| 1/2*x+3*cos(x)+2=0
|
| 2*x5 –8*x2+0.8=0
|
| 8*x3+5*x2–17*x-1=0
|
|
| 8*x2+5*x-1–17=0
|
| 5*x2+3*cos(x)–4=0
|
| 8*x3+ ln(x2) =0
|
|
| 5*x3–6*x+0.2=0
|
| 3–7*cos2(x)*sin(x)– –3* sin3(x)=0
|
| ln(7*x)–x-1=0
|
|
| 5*x4–6*x2+0.5=0
|
| 8*sin(2x)– 3*cos2(x)–4=0
|
| 1/4*x4–3*cos(x)+2=0
|
|
| 5*x3–6*x2+3=0
|
| x2+ sin(x)–5*x3=0
|
| 2*x4+x3–3*sin(x)=0
|
Задание 2
Решить уравнение полиномиального вида, заданного функцией F(x): = A0+A1*x+A2*x2+A3*x3. Значения коэффициентов взять в соответствии со своим вариантом. Варианты заданий приведены в табл.4.13.
Таблица 4.13
Варианты заданий
| № вар.
| Значения коэффициентов
|
| А0
| А1
| А2
| А3
|
|
| -5
|
|
|
|
|
|
|
|
|
|
|
| -55
|
|
|
|
|
|
| -8
| -10
|
|
|
| -3
| -11
|
|
|
|
| -5
|
| -9
|
|
|
| -52
|
| -6
|
|
|
|
| -33
|
|
|
|
|
|
|
|
|
|
| -4
|
|
|
|
|
| -12
|
|
|
|
|
| -7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -11
|
|
|
|
|
|
|
|
|
| -7
|
| -9
|
|
|
| -3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -12
|
|
|
|
|
| -2
|
|
|
|
| -5
|
| -11
|
|
|
|
| -2
|
|
|
|
|
| -5
|
|
|
| -4
|
|
|
|
|
| -6
|
| -2
|
|
|
|
|
|
| -9
|
Задание 3
Решить систему линейных алгебраических уравнений матричным методом. Варианты заданий приведены в табл. 4.14.
Таблица 4.14
Варианты заданий
| № вар
| Задание
| № вар
| Задание
| № вар
| Задание
|
|
|
|
|
|
|
|
|
| 5x1+3x2-4x3+x4=8
-3x1+8x2-4x3-2x4=-5
x1-12x2+2x3-2x4=-3
-3x1+7x2+x3-4x4=-6
|
| 0.5x+0, 5x2-4x3+x4=8.5
3x1-8x2-4x3-x4=-12
6x1-7x2+2x3-2x4=-5
-3x1+7x2+5x3-4x4=11
|
| -x1+2x2+2x3+8x4=10
-9x1+x2+3x3-7x4=0
11x1+5x2-2x3+5x4=7
x1+3x2+5x3-6x4=4
|
|
| 9x1+5x2-4x3+x4=6
-x1+6x2-3x3-5x4=-2
x1-2x2+2x3-2x4=-3
-5x1+3x2+x3-x4=-1
|
| 2x1-6x3+x4=3
11x1+8x2-x3-2x4=16
x1-2x2+2x3-4x4=0
-4x1+x3-4x4=-10
|
| -4x1-5x2+4x3-5x4=-11
x1-x2-2x3+8x4=7
-4x1+7x2-4x3-4x4=9
9x1+4x2-2x3-12x4=3
|
|
| -5x1+4x2-4x3-x4=-4
-x1+6x2-3x3-5x4=-2
x1-3x2+5x3+6x4=7
-4x1+x2+x3-4x4=-2
|
| 15x1+13x2-4x3+x4=20
5x1+8x2-4x3=5
3x1-x2+3x3-2x4=-3
-x1+4x2+x3-4x4=0
|
| -10x1-9x2+x3+2x4=-2
4x1+5x2+4x3+12x4=6
-8x1-2x2-x3+9x4=15
4x1-3x2-3x3-2x4=-3
|
|
| x1+8x+4x3-2x4=7
7x1-x2+x3-9x4=10
6x1-3x2+x3+12x4=4
11x1-9x2-5x3+6x4=0
|
| 10x1+4x3+x4=18
9x1+8x2-4x3-11x4=0
x1-12x2+2x3-2x4=-5
x1+7x2+x3-x4=6
|
| -2x1-6x2+5x3+9x4=-9
6x1+8x2-4x3-2x4=-5
-3x1-4x2-8x3+7x4=13
x1+2x2-7x3+9x4=-4
|
|
| -2x1+2x2-9x3+5x4=6
x1-2x2+10x3-7x4=-4
-11x1+x2+9x3-2x4=1
3x1+7x2-x3-x4=3
|
| 4x1+x2-4x3+x4=8
-3x1+8x2-4x3-2x4=-5
x1+4x2+2x3-2x4=7
-1.5x1+3x2+x3-4x4=-6
|
| -8x1+2x2+x3-x4=0
x1+10x2-6x3+x4=-10
5x1-2x2+9x3-4x4=-8
-7x1-7x2-5x3+3x4=2
|
|
| -x1-5x2-6x3+7x4=0
3x1-7x2-2x3-2x4=-2
2x1+10x2+4x3+2x4=5
-13x1-x2-8x3-3x4=-1
|
| 5x1+3x2-4x3+x4=8
x1+x2-4x3-5x4=3
5x1-2x2+4x3-2x4=-3
-x1+7x2-4x4=0
|
| -8x1+2x2+x3-x4=0
x1+10x2-6x3+x4=-10
5x1-2x2+9x3-4x4=-8
-7x1-7x2-5x3+3x4=2
|
|
| -5x1+3x2-x3+5x4=-2
7x1-6x2-7x3+x4=3
x1+x2-11x3-5x4=9
5x1-14x2+4x3-6x4=7
|
| 5x1+3x2-4x3+x4=8
-3x1+6x2-4x3=-7
x1-9x2+2x3+4x4=0
3x1-2x2+2x3-2x4=-7
|
| 6x1-4x2+3x3+5x4=-2
-4x1+7x2-5x3-4x4=-4
2x1-2x2+6x3-72x4=-4
-2x1+7x2+x3-5x4=-3
|
Окончание табл. 4.14
|
|
|
|
|
|
|
|
| 10x1+6x2-8x3+2x4=4
6x1-4x2+8x3+4x4=10
-2x1+6x2-4x3+4x4=6
6x1-15x2-2x3+8x4=3
|
| 7x1-6x2-7x3+x4=3
x1-6x2+2x3-2x4=-1
-3x1+7x2+x3-4x4=-6
2x1+10x2+4x3+2x4=5
|
| 3х1+2x2-9x3+2x4=0
6x1+9x2-5x3-x4=-3
3x1-4х2+x3-7x4=-5
2x1+7x2+2x3-3x4=-6
|
|
| 2.5x1+3x2-4x3+x4=0
-3x1+8x2-2x4=-3
3x1-2x2+2x3-2x4=-7
-3x1+7x2+x3-4x4=-2
|
| -3x2-x3+x4=-3
-x1+5x2+2x3-2x4=-5
x1-2x2+6x3-2x4=2
-3x1+x2+x3-4x4=-8
|
| 5x1+2x2-x3+3x4=7
-7x1+6x2-5x3-7x4=-5
x1-12x2+2x3-2x4=-3
-4x1+7x2+x3-7x4=-6
|
|
| x1+3x2+4x3+x4=8
-3x1+2x2-4x3-2x4=-5
x1-6x2+2x3-2x4=-1
-3x1+7x2+x3+4x4=12
|
| x1+3x2+2x3+x4=4
-3x1+x2-4x3-2x4=-5
x1-5x2+2x3+3x4=9
-3x1+4x2+x3-7x4=-5
|
| 1. 4x1+x2-6x3+x4=5
4x1+8x2-2x3-3x4=-5
-x1-12x2+3x3-2x4=-3
-5x1+7x2+3x3-3x4=-6
|
Задание 4
Решить систему линейных алгебраических уравнений из предыдущего задания при помощи функции lsolve.
Задание 5
Решить систему уравнений двумя способами (с использованием функции find и с использованием стандартной функции minerr. Варианты заданий приведены в табл.4.15.
Таблица 4.15
Варианты заданий
| № вар
| Задание
| № вар
| Задание
| № вар
| Задание
|
|
|
|
|
|
|
|
|
| 
|
| 
|
| 
|
|
| 
|
| 
|
| 
|
|
| 
|
| 
|
| 
|
|
| 
|
| 
|
| 
|
Окончание табл. 4.15