РАСЧЕТ УСТОЙЧИВОСТИ ОТКОСОВ
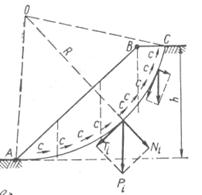
Метод круглоцилиндрических поверхностей скольжения. Этот метод широко применяют на практике, так как он дает некоторый запас устойчивости и основан на опытных данных о форме поверхностей скольжения при оползнях вращения, которые на основании многочисленных замеров в натуре (например, Шведской геотехнической комиссии) принимают за круглоцилиндрические, при этом самое невыгодное их положение определяется расчетом. Принятие определенной формы поверхностей скольжения и ряда других допущений (о чем будет сказано ниже) делает этот метод приближенным. Допустим, что центр круглоцилиндрической поверхности скольжения оползающей призмы находится в точке О (рис. 23). Уравнением равновесия будет Σ М 0 = 0. Для составления уравнения моментов относительно точки вращения О разбивают призму скольжения АВС вертикальными сечениями на ряд отсеков и принимают вес каждого отсека условно приложенным в точке пересечения веса отсека Рi с соответствующим отрезком дуги скольжения, а силами взаимодействия по вертикальным плоскостям отсека (считая, что давления от соседних отсеков равны по величине, а по направлению противоположны) пренебрегают. Раскладывая далее силы веса Рi на направление радиуса вращения и ему перпендикулярное, составляют уравнение равновесия, приравнивая нулю момент всех сил относительно точки вращения:
Σ TiR – Σ Ni tg R + cLR = 0. (66)
Рис. 23.Схема действия сил при расчете откоса по кругло-цилиндрическим поверхностям скольжения Сокращая выражение (66) на R, получим Σ Ti – Σ Ni tgφ + cL = 0, (67)
где L — длина дуги скольжения АС; φ, с — угол внутреннего трения и сцепление грунта; Ti и Ni — составляющие давления от веса отсеков
Ti = Рi sinα i; Ni = Рi cosα i.
За коэффициент устойчивости откоса принимают отношение момента сил удерживающих к моменту сил сдвигающих η = М уд/ М сдв = (Σ Ni tgφ + cL) /Σ Ti. (68)
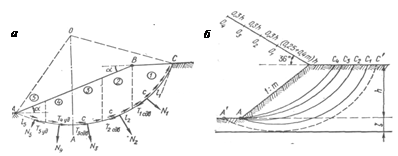
Однако решение поставленной задачи определением коэффициента устойчивости для произвольно выбранной дуги поверхности скольжения не заканчивается, так как необходимо из всех возможных дуг поверхностей скольжения выбрать наиболее опасную. Последнее выполняется путем попыток, задаваясь различными положениями точек вращения О; для уменьшения числа попыток существуют некоторые правила, например, проф. Феллениуса (рис. 24, б, где указано положение опасных дуг скольжения) и др. Для ряда намеченных центров дуг поверхностей скольжения определяют необходимое по условию устойчивости сцепление, соответствующее предельному равновесию заданного откоса, по выражению, вытекающему из соотношения (67), а именно:
c = (Σ Ti – Σ Ni tg φ)/ L. (69)
Далее, из всех возможных центров скольжения выбирают тот, для которого требуется максимальная величина сил сцепления. Этот центр принимают за наиболее опасный и для него по формуле (68) вычисляют коэффициент устойчивости η . Обычно считают, что при значении η > 1, 1…1, 5 откос будет устойчивым. Формула (61) будет справедлива лишь для тех случаев, когда дуга поверхности скольжения во всех своих частях является ниспадающейв сторону возможного смещения откоса или склона или (в случае скольжения по цилиндрической поверхности) когда все отсеки кривой скольжения располагаются по одну сторону от направления вертикального радиуса ОА (рис. 24, а).
Рис. 24.К расчету устойчивости откоса по круглоцилиндрическим а – схема сил, действующих по поверхности скольжения; б – положение опасных дуг скольжения
|