НА ЕГО ПОВЕРХНОСТИ

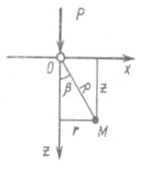
Общие положения. Распределение напряжений в основании в большой мере зависит от формы фундамента в плане. Поскольку в промышленном и гражданском строительстве обычно используются ленточные, прямоугольные или круглые фундаменты, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.

Напомним, что распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Полученные методами теории упругости напряжения соответствуют стабилизированному состоянию, т. е. такому периоду времени, когда все процессы консолидации и ползучести грунтов основания под действием приложенной нагрузки уже завершились и внешняя нагрузка оказывается полностью уравновешенной внутренними силами (эффективными напряжениями в грунте). Кроме того, принимается, что зоны развития пластических деформаций, возникающие в основании у краев фундамента (вследствие краевого эффекта), незначительны и не оказывают заметного влияния на распределение напряжений в основании.

Приведем общий ход решения задач о распределении напряжений в упругом полупространстве под действием местной нагрузки. В основе общего хода решения задач о распределении напряжений лежит решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885 г. Ж. Буссинеском. Это решение позволяет определить все компоненты напряжений и деформаций в любой точке полупространства М от действия силы Р (рис. 21, а). Поскольку для практических расчетов наибольшее значение имеют сжимающие напряжения, то их можно определить по следующей зависимости:

σ _z= (K / z ²) P, (59)

где

K =(3/2π)× (1/((1+(r / z)²)^5/2 .

 

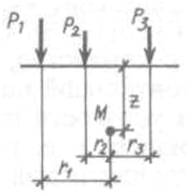
Используя принцип суперпозиции, можно определить значение вертикального сжимающего напряжения в точке М при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 21, б)

σ _z= (K ₁/ z ²) P ₁ + (K₂ / z ²) P₂+…+ (K_n / z ²) P_n (60)

а б

Рис. 21. Расчетная схема определения напряжений:

а – задача Буссинеска; б – при действии нескольких сосредоточенных сил

 

Используя приведенные выражения (59), (60), можно достаточно просто определить напряжения в любой точке основания при любой форме фундамента и заданном законе распределения нагрузки. Как правило, в гражданских и промышленных сооружениях фундаменты зданий имеют прямоугольную форму с шириной b и длиной l, если отношение (l / b) > 10 то фундамент рассматривается как ленточный.

При расчетах напряжений под фундаментами зданий используют формулу

 

σ _z= α p, (61)

 

где α — коэффициент влияния; p — давление под подошвой фундамента.

Коэффициент влияния α зависит от параметров η = (l / b) и m= 2 z / b и определяют по таблицам [1] или приложению А.