Виды средних и способы их вычисления
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (при различных значениях m):
m Σ хmi
где х — среднее значение исследуемого явления; m — показатель степени средней; х — текущее значение (вариант) осредняемого признака; n — число признаков. В зависимости от значения показателя степени т различают следующие виды степенных средних: при m =-1 — средняя гармоническая Хгар; при m = 0 — средняя геометрическая Хг; при m = 1 — средняя арифметическая Хар; при m = 2 — средняя квадратическая Хкв; при m = 3 — средняя кубическая Хкуб; При использовании одних и тех же исходных данных, чем больше в формуле (7.1), тем больше значение средней величины: Хгар ≤ Хг≤ Хар ≤ Хкв ≤ Хкуб (6.2) Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистике правилом мажорантности средних. Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципами суммирования и взвешивания. Помимо степенных средних в статистической практике используются средние структурные, в качестве которых рассматриваются мода и медиана. Остановимся подробнее на степенных средних.
|


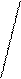 n
n - i=1 (6.1)
- i=1 (6.1) х = n
х = n


