Пример 1. Пусть имеются следующие данные о заработной плате рабочих сдельщиков: Заработная плата, тыс
Пусть имеются следующие данные о заработной плате рабочих сдельщиков:
По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются по нескольку раз. Так варианта Х1 встречается в совокупности 2 раза, а варианта Х3 – 16 раз. Необходимо исчислить среднюю заработную плату одного рабочего
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих. Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. Рассмотрим расчет средней арифметической для таких рядов. Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты осредняемого признака (продукции за смену) представлены не одним числом, а в виде интервала «от – до». Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы от 5 до 7 шт., и т.д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значение вариант, т.е. образовались закрытые интервалы.
Исчисление средней по сгруппированным данным проводиться по формуле средней арифметической взвешенной.
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значений интервала. Так, для первой группы дискретная величина Х будет равна:
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:
Итак, все рабочие произвели 750 штук изделий за смену, а каждый в среднем произвел по 7, 5 штук. Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами. Допустим, что имеются следующие данные о производстве продукции за смену.
В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше. Свойства средней арифметической значительно упрощает вычисления: · если увеличить или уменьшить все варианты осредняемого признака на какое-либо одно и то же число, то объем средней величины соответственно увеличится или уменьшится на это же число; · если увеличить или уменьшить все варианты осредняемого признака в какое-либо число раз, то объем средней величины соответственно увеличится или уменьшится в это же количество раз; · от увеличения или уменьшения веса каждого варианта признака в какое-либо число раз величина средней не изменится. Применение данного свойства с практической точки зрения удобно, если необходимо проанализировать совокупность со значительным количеством элементов, а частота элементов выражена многозначными числами. Если частоты элементов равны между собой, то среднюю можно рассчитать как невзвешенную; · как следствие предыдущего свойства можно сказать, что величина средней зависит не от абсолютных значений веса отдельных элементов, а от их доли в общей сумме весов, т.е. если не известны абсолютные выражения весов элементов, а известны пропорции между ними, то они могут использоваться для расчета средней; · средняя арифметическая совокупности, состоящей из их постоянных величин, равна этой постоянной: х = х при х = const.
Ø средняя гармоническая (простая и взвешенная);
Взвешенная, где w — значение сводного, объемного, выступающего как признак-вес показателя:
|

 Число одинаковых значений признака в рядах распределения называются частотой (или весом) и обозначается символом f.
Число одинаковых значений признака в рядах распределения называются частотой (или весом) и обозначается символом f. ; среднюю заработанную плату одного рабочего
; среднюю заработанную плату одного рабочего  , где А – заработная плата всех рабочих, N – число рабочих:
, где А – заработная плата всех рабочих, N – число рабочих:
 .
. и т.д.
и т.д. .
.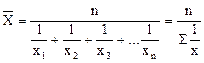 простая
простая .
.


