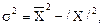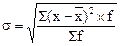Пример 1. Поясним правила сложения на примере

Поясним правила сложения на примере. Имеются следующие данные о производительности ткачей за час работы.

Исчислим:

1) групповые дисперсии;

2) среднюю из групповой дисперсии;

3) межгрупповую дисперсию;

4) общую дисперсию.

1. Для расчета групповых дисперсий исчислим среднее по каждой группе:

X₁ = = 15 т.; X₂ = = 21 т.

Подставив полученные значения в формулу, получим:

Таблица

Табельный номер ткача	Изготовлено ткани трехстаночниками за 1 час (х)	х –хi	(х – хi)2	Табельный номер ткача	Изготовлено ткани четырехстаночникамм за 1 час (х)	х – хi	(х – хi)2
		–2				–3
		–1				–2
						–1
Итого

 

2. Рассчитаем среднюю из групповых (частных) дисперсий:

3. Исчислим межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:

Затем рассчитаем межгрупповую дисперсию:

d² = 18 м².

4. Исчислим общую дисперсию по правилу сложения дисперсии:

² = _i + d = 3, 16 + 9 = 12, 16.

Проверим полученный результат, исчислив общую дисперсию обычным способом:

 

Расчет обычным способом привел к аналогичному результату, но оказался более трудоемким.

 

СВОЙСТВА ДИСПЕРСИИ

1) уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет;

2) уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину (А) дисперсии не изменяет;

3) уменьшение или увеличение каждого значения признака в какое-то число раз (К) соответственно уменьшает или увеличивает дисперсию в (К2) раз, а среднее квадратическое отклонение – в (К) раз;

4) дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности средней и произвольной величинами:

Если число А равно нулю, то приходим к следующему равенству:

т.е. дисперсия признака равна разности между квадратом значения признака и квадратом средней. Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другим.

 

Ø Среднее квадратическое отклонение (s) представля­ет собой корень квадратный, извлеченный из дисперсии. Различают простое и взвешенное среднее квадра­тическое отклонение.

Простое (невзвешенное) среднее квадратическое от­клонение определяется по формуле

 

Взвешенное среднее квадратическое отклонение опре­деляется по формуле