Дисперсия альтернативного признака
Выше был рассмотрен расчет показателей вариации для количественных признаков. Но наряду с вариацией количественных признаков может ставиться задача оценки вариация качественных признаков. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественных признаков. Например, при изучении качества изготовленной продукции можно разделить ее на две группы: годную и бракованную. В таком случае будем иметь дело с альтернативным признаком. Можно считать, что эквивалентом качественного признака будет переменная, которая принимает значение 1 или 0, причем значение 1 она принимает в том случае, когда обследуемая единица обладает данным признаком, а значение 0, когда не обладает им. Допустим, общее число единиц совокупности равно п. Число единиц, обладающих данным признаком - f, тогда число единиц, не обладающих данным признаком, будет равно п-f. Учитывая изложенное, построим ряд распределения по качественному признаку:
Средняя арифметическая такого ряда равна:
т.е. равна относительной частоте (частости), которую можно обозначить через р, тогда Таким образом, доля единиц, обладающих данным признаком, равна р; соответственно доля единиц, не обладающих данным признаком, равна q; р+q= 1. Тогда дисперсия альтернативного признака определяется по формуле
Среднее квадратическое отклонение альтернативного признака:
Ø Эмпирический коэффициент детерминации (ή 2), отражающий определенную изменением признака-фактора долю вариации результативного признака: ή 2 = δ 2 / s2 общ
s2 общ — общая дисперсия δ 2— межгрупповая дисперсия;
Ø Эмпирическое корреляционное отношение (ή), определяющее тесноту связи между изменением признака-фактора и последующим изменением признака-результата, представляет собой корень из коэффициента детерминации ή = √ (δ 2 / s2 общ) Чем ближе к единице значение эмпирического корреляционного отношения, тем теснее связь между изменением признака-фактора и признака-результата. Критерии согласия Критерии согласия - особые статистические показатели, характеризующие соответствие эмпирического и теоретического распределений. Известны критерии согласия К. Пирсона, В.И. Романовского, А.Н. Колмогорова, Б.С. Ястремского.
|

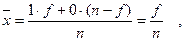
 = р.
= р.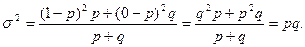
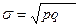 .
.


