Общий метод линеаризации
Допустим, что звено описывается некоторым нелинейным дифференциальным уравнением вида
Для составления такого уравнения нужно использовать соответствующую отрасль технических наук (например электротехнику, механику, гидравлику и т. п.), изучающую этот конкретный вид устройства. Основанием для линеаризации служит предположение о достаточной малости отклонений всех переменных, входящих в уравнение динамики звена, так как именно на достаточно малом участке криволинейную характеристику можно заменить отрезком прямой. Отклонения переменных отсчитываются при этом от их значений в установившемся процессе или в определенном равновесном состоянии системы. Пусть, например, установившийся процесс характеризуется постоянным значением переменной Х1, которое обозначим Х10. В процессе регулирования (рис. 2.3) переменная Х1 будет иметь значения
Далее можно записать: Все отклонения предполагаются достаточно малыми. Это математическое предположение не противоречит физическому смыслу задачи, так как сама идея автоматического регулирования требует, чтобы все отклонения регулируемой величины в процессе регулирования были достаточно малыми. Установившееся состояние звена определяется значениями Х10, Х20 и F0. Тогда уравнение (2.1) может быть записано для установившего состояния в виде
Разложим левую часть уравнения (2.1) в ряд Тейлора
где D – члены высшего порядка. Индекс 0 при частных производных означает, что после взятия производной в её выражение надо подставить установившееся значение всех переменных В состав членов высшего порядка в формуле (2.3) входят высшие частные производные, умноженные на квадраты, кубы и более высокие степени отклонений, а также произведения отклонений. Они будут малыми высшего порядка по сравнению с самими отклонениями, которые являются малыми первого порядка. Уравнение (2.3) является уравнением динамики звена, так же как (2.1), но записано в другой форме. Отбросим в этом уравнении малые высшего порядка, после чего из уравнения (2.3) вычтем уравнения установившегося состояния (2.2). В результате получим следующее приближённое уравнение динамики звена в малых отклонениях:
В это уравнение все переменные и их производные входят линейно, то есть в первой степени. Все частные производные представляют собой некоторые постоянные коэффициенты в том случае, если исследуется система с постоянными параметрами. Если же система имеет переменные параметры, то уравнение (2.4) будет иметь переменные коэффициенты. Рассмотрим только случай постоянных коэффициентов. Получение уравнения (2.4) является целью проделанной линеаризации. В теории автоматического регулирования принято записывать уравнения всех звеньев так, чтобы в левой части уравнения была выходная величина, а все остальные члены переносятся в правую часть. При этом все члены уравнения делятся на коэффициент при выходной величине. В результате уравнение (2.4) принимает вид
где введены следующие обозначения
Кроме того, для удобства принято все дифференциальные уравнения записывать в операторной форме с обозначениями
Тогда дифференциальное уравнение (2.5) запишется в виде
Эту запись будем называть стандартной формой записи уравнения динамики звена. Коэффициенты Т1 и Т2 имеют размерность времени – секунды. Это вытекает из того, что все слагаемые в уравнении (2.8) должны иметь одинаковую размерность, а например, размерность Коэффициент k1 имеет размерность выходной величины, деленную на размерность входной. Он называется коэффициентом передачи звена. Для звеньев, у которых выходная и входная величины имеют одинаковую размерность, используются также следующие термины: коэффициент усиления – для звена, представляющего собой усилитель или имеющего в своем составе усилитель; передаточное число – для редукторов, делителей напряжения, масштабирующих устройств и т. п. Коэффициент передачи характеризует статические свойства звена, так как в установившемся состоянии Из рисунка видно, что проделанная выше линеаризация уравнения справедлива для процессов регулирования, захватывающих такой участок характеристики АВ, на котором касательная мало отличается от самой кривой. Кроме того, отсюда вытекает другой, графический способ линеаризации. Если известна статическая характеристика и точка C, определяющая установившееся состояние, около которого происходит процесс регулирования, то коэффициент передачи в уравнении звена определяется графически из чертежа по зависимости k1 = tg Размерность коэффициента k2 равна размерности коэффициента передачи k1, умноженной на время. Поэтому часто уравнение (2.8) записывают в виде
где
Коэффициент k3 представляет собой коэффициент передачи по внешнему возмущению. В качестве примера линеаризации рассмотрим электрический двигатель, управляемый со стороны цепи возбуждения (рис. 2.4).
Для нахождения дифференциального уравнения, связывающего приращение скорости с приращением напряжения на обмотке возбуждения, запишем закон равновесия электродвижущих сил (эдс) в цепи возбуждения, закон равновесия эдс в цепи якоря и закон равновесия моментов на валу двигателя:
Во втором уравнении для упрощения опущен член, соответствующий эдс самоиндукции в цепи якоря. В этих формулах RВ и RЯ – сопротивления цепи возбуждения и цепи якоря; ІВ и ІЯ – токи в этих цепях; UВ и UЯ – напряжения, приложенные к этим цепям; wВ – число витков обмотки возбуждения; Ф – магнитный поток; Ω – угловая скорость вращения вала двигателя; М – момент сопротивления от внешних сил; J – приведенный момент инерции двигателя; СЕ и Допустим, что до появления приращения напряжения, приложенного к обмотке возбуждения, существовал установившийся режим, для которого уравнения (2.10) запишутся следующим образом:
Если теперь напряжение возбуждения получит приращение UВ = UВ0 + Δ UВ, то все переменные, определяющие состояние системы, также получат приращения. В результате будем иметь: ІВ = ІВ0 + Δ ІВ; Ф = Ф0 + Δ Ф; IЯ = IЯ0 + Δ ІЯ; Ω = Ω 0 + Δ Ω. Подставляем эти значения в (2.10), отбрасываем малые высшего порядка и получаем:
Вычитая из уравнений (2.12) уравнения (2.11), получим систему уравнений для отклонений:
Совместное решение системы (2.13) даёт
где коэффициент передачи,
электромагнитная постоянная времени цепи возбуждения, с,
где LB = a wB – динамический коэффициент самоиндукции цепи возбуждения; электромагнитная постоянная времени двигателя, с,
Из выражений (2.15) – (2.17) видно, что рассматриваемая система является по существу нелинейной, так как коэффициент передачи и «постоянные» времени, на самом деле – не постоянны. Их можно считать постоянными только приближенно для какого-то определенного режима при условии малости отклонений всех переменных от установившихся значений. Интересным является частный случай, когда в установившемся режиме UB0 = 0; ІB0 = 0; Ф0 = 0 и Ω 0 = 0. Тогда формула (2.14) приобретает вид
В этом случае статическая характеристика будет связывать приращение ускорения двигателя
Контрольные вопросы 1. Опишите линейные и нелинейные САР. 2. Дайте понятие линеаризации и объясните ее необходимость. 3. Изложите общий метод линеаризации. 4. Какова стандартная форма записи дифференциальных уравнений?
|

 В большинстве случаев можно линеаризовать нелинейные зависимости, используя метод малых отклонений или вариаций. Для рассмотрения его обратимся к некоторому звену системы автоматического регулирования (рис. 2.2). Входная и выходная величины обозначены через X1 и X2, а внешнее возмущение – через F(t).
В большинстве случаев можно линеаризовать нелинейные зависимости, используя метод малых отклонений или вариаций. Для рассмотрения его обратимся к некоторому звену системы автоматического регулирования (рис. 2.2). Входная и выходная величины обозначены через X1 и X2, а внешнее возмущение – через F(t). . (2.1)
. (2.1) где
где  обозначает отклонение переменной X1 от установившегося значения Х10.
обозначает отклонение переменной X1 от установившегося значения Х10. Аналогичные соотношения вводятся для других переменных. Для рассматриваемого случая имеем:
Аналогичные соотношения вводятся для других переменных. Для рассматриваемого случая имеем:  а также
а также  .
.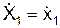 ;
;  и
и  , так как
, так как  и
и 
 . (2.2)
. (2.2)
 (2.3)
(2.3)
 .
. (2.4)
(2.4) (2.5)
(2.5) . (2.6)
. (2.6) и т.д. (2.7)
и т.д. (2.7) , (2.8)
, (2.8) (или px2) отличается от размерности х2 на секунду в минус первой степени (
(или px2) отличается от размерности х2 на секунду в минус первой степени ( ). Поэтому коэффициенты Т1 и Т2 называют постоянными времени.
). Поэтому коэффициенты Т1 и Т2 называют постоянными времени. . Следовательно, он определяет крутизну статической характеристики при малых отклонениях. Если изобразить всю реальную статическую характеристику звена
. Следовательно, он определяет крутизну статической характеристики при малых отклонениях. Если изобразить всю реальную статическую характеристику звена  , то линеаризация дает
, то линеаризация дает  или
или  касательной в той точке C (см. рис. 2.3), от которой отсчитываются малые отклонения х1 и х2.
касательной в той точке C (см. рис. 2.3), от которой отсчитываются малые отклонения х1 и х2. , (2.9)
, (2.9) – постоянная времени.
– постоянная времени. Постоянные времени Т1, Т2 и Т3 определяют динамические свойства звена. Этот вопрос будет рассмотрен подробно ниже.
Постоянные времени Т1, Т2 и Т3 определяют динамические свойства звена. Этот вопрос будет рассмотрен подробно ниже. ;
; ; (2.10)
; (2.10) .
. (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13) В этих уравнениях введен коэффициент пропорциональности между приращением потока и приращением тока возбуждения
В этих уравнениях введен коэффициент пропорциональности между приращением потока и приращением тока возбуждения  определяемый из кривой намагничивания электродвигателя (рис. 2.5).
определяемый из кривой намагничивания электродвигателя (рис. 2.5). , (2.14)
, (2.14) ,
, ; (2.15)
; (2.15) (2.16)
(2.16) . (2.17)
. (2.17) . (2.18)
. (2.18)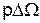 и приращение напряжения в цепи возбуждения.
и приращение напряжения в цепи возбуждения.


