УКАЗАНИЯ И РЕШЕНИЯ
1. Монеты. Рассмотрим подзадачу, в которой требуется найти наименьшее количество монет, которыми можно выдать сумму i, i £ S. Обозначим решение этой подзадачи через f(i). Если известны все значения f(j), 1 £ j £ i, то легко найти f(i + 1): f(i + 1) = По умолчанию положим f(0) = 0, так как сумму в 0 копеек можно выдать 0 монетами. Значения решений для подзадач f(i) храним в некотором числовом массиве m. Пример. Пусть имеются монеты достоинством 1, 2 и 5 копеек. Значение искомой суммы равно S = 9. Значение элементов массива m имеет вид:
Сумму в 9 копеек можно выдать так: 9 = 5 + 2 + 2.
2. Задача о загрузке. Обозначим через f(i, w) максимальную стоимость, которую можно получить имея лишь первые i грузов и грузоподъемность w. Если i - ый груз не использовался при подсчете f(i, w), то f(i, w) = f(i – 1, w). Иначе значение f(i, w) равно f(i – 1, w - wi) + ci. Отсюда получаем рекуррентное соотношение: f(i, w) = max(f(i – 1, w), f(i – 1, w - wi) + ci), i > 1 f(1, wi) = ci Пример. Рассмотрим тест, в котором имеются четыре груза со следующими характеристиками:
Положим изначально m[0] = 0, m[ i ] = -1, i = 1, …, 9. Значения f(i, w) занесем в следующую таблицу:
Реализация. Положим MAX = w + 1. Положим m[0] = 0, m[ i ] = -1, i = 1, …, MAX – 1. Для каждого груза весом weight и стоимостью cost пересчитываем значения элементов массива m начиная с конца.
#include <stdio.h> #include <memory.h> #define MAX 10
int i,j,n,w; int weight,cost,m[MAX];
void main(void) { memset(m,-1,sizeof(m));m[0] = 0; scanf("%d %d",&n,&w); for(i=0;i<n;i++) { scanf("%d %d",&weight,&cost); for(j = MAX - 1; j >= weight; j--) if ((m[j - weight] >= 0) && (m[j] < m[j - weight] + cost)) m[j] = m[j - weight] + cost; } printf("%d\n",m[w]); }
3. Доллары [Вальядолид, 147, 357, 674]. Обозначим через f(k, n) количество способов составить сумму n из первых k номиналов монет. Оно равно количеству способов составить сумму n первыми (k – 1) номиналами плюс количество способов составить сумму (n – ak) k номиналами. Имеем соотношение: f(k, n) = f(k – 1, n) + f(k, n – ak)
Изначально положим f(0, 0) = 1, f(n, 0) = 0, n > 0. Пример. Сумму s = 20 можно выдать 4 способами: 1) 20 2) 10 + 10 3) 10 + 5 + 5 4) 5 + 5 + 5 +5
Остальные номиналы не повлияют на результат для суммы в 20 центов. Реализация. Ячейка mas[ i ] будет содержать количество способов, которыми можно выдать сумму i. Размер массива установим MAX = 30001. Номиналы монет (в центах) занесем в массив coins. Динамически пересчитываем массив mas для каждого номинала (всего 11 номиналов) согласно соотношению, приведенному в анализе алгоритма. #include <stdio.h> #include <memory.h>
const int MAX = 30001; double v; int i,j,n; long long mas[MAX]; int coins[11] = {5,10,20,50,100,200,500,1000,2000,5000,10000};
void main(void) { memset(mas,0,sizeof(mas)); mas[0] = 1; for(i=0;i<11;i++) { for(j=coins[i];j<MAX;j++) mas[j] += mas[j-coins[i]]; }
Читаем входные суммы v, преобразовываем их в целое число центов n и печатаем результат mas[ n ] в соответствии с требуемым форматом.
while(scanf("%lf",&v),v>0) { n = (int)(v*100+0.1); printf("%6.2lf%17lld\n",v,mas[n]); } }
4. Оптимальное умножение матриц [Вальядолид, 348]. Обозначим через A ij произведение матриц A i * A i +1 * … * A j -1 * A j (1 £ i £ j £ n), через m[ i, j ] минимальное количество умножений, необходимое для вычисления A ij. Стоимость вычисления всего произведения A1 n будет храниться в m[1, n ]. Значения m[ i, i ] = 0, поскольку A ii = A i и для его нахождения вычисления не нужны. Количество столбцов матрицы A i равно количеству строк матрицы A i +1. Это значение хранится в p[ i ]. Количество строк матрицы А1 находится в p[0], а количество столбцов A n – в p[ n ]. Предположим, что при оптимальной расстановке скобок в произведении A i * … * A j последней операцией умножения будет (A i * … * A k) * (A k+1 * … * A j). Значение m[ i, j ] равно сумме минимальной стоимости вычислений A ik и A k +1 j плюс стоимость умножения этих двух матриц: m[ i, j ] = m[ i, k ] + m[ k +1, j ] + p[ i -1] * p[ k ] * p[ j ] При этом число k может принимать только j – i разных значений: i, i + 1, …, j – 1. Поскольку только одно из них является оптимальным, то необходимо перебрать все эти значения и выбрать наилучшее. Получим рекуррентную формулу: m[ i, j ] = Для запоминания оптимального умножения положим s[ i, j ] = k, если при оптимальном вычислении A i * … * A j последней операцией будет умножение A i * … * A k на A k +1 * … * A j. Пример. Рассмотрим третий тест. Данные о размерах входных матриц сохраняются в массиве p: Минимальная стоимость вычисления матриц A ij хранится в ячейках массива m[ i, j ]:
Соответствующие значения матрицы s:
Для умножения шести входных матриц достаточно выполнить m[1,6] = 15125 операций умножения. Оптимальная последовательность умножений имеет вид: A16 = (s[1,6] = 3) = A13 * A46 = (s[1,3] = 1, s[4,6] = 5) = (A11 * A23) * (A45 * A66) = (s[2,3] = 2, s[4,5] = 4) = (A11 * (A22 * A33)) * ((A44 * A55) * A66) = (A1 * (A2 * A3)) * ((A4 * A5) * A6) Реализация. Переменная INF обозначает число «бесконечность», MAX – 1 содержит максимально возможное число матриц в произведении. Объявим строковый массив Stroka, в котором храним числа от 0 до 10 в виде строк. Объявим массивы m, s, p, описанные выше. В переменной Answer будем накапливать результат.
#define INF 0x3F3F3F3F #define MAX 11 string Stroka[11] = {"0","1","2","3","4","5","6","7","8","9","10"}; int m[MAX][MAX], s[MAX][MAX], p[MAX]; string Answer;
Функция Mult находит минимальное количество умножений, необходимое для вычисления A ij = A i * A i +1 * … * A j -1 * A j, которое сохраняем в ячейке m[ i, j ].
int Mult(int i, int j) { int k, temp; if (m[i][j] == INF) for (k = i; k <= j - 1; k++) { temp = Mult(i,k) + Mult(k+1,j) + p[i-1] * p[k] * p[j]; if (temp < m[i][j]) { m[i][j] = temp; s[i][j] = k; } } return m[i][j]; }
Функция Print(i, j) выводит оптимальное произведение матриц A i * A i +1 * … * A j -1 * A j согласно формату вывода.
string Print(int i, int j) { if (i == j) return "A" + Stroka[i]; return "(" + Print(i,s[i][j]) + " x " + Print(s[i][j]+1,j) + ")"; }
Основной цикл программы. Переменная cs содержит номер теста.
cs = 1; while(scanf("%d",&n),n>0) {
Присвоим всем ячейкам массива m значения «бесконечность».
memset(m,0x3F,sizeof(m));
Читаем размеры входных матриц, сохраняем их в массиве p. Положим m[ i, i ] = 0.
for(i = 1; i <= n; i++) { scanf("%d %d",&p[i-1],&p[i]); m[i][i] = 0; }
Вычисляем результат – ищем оптимальное произведение матриц A1 * A2 * … * A n -1 * A n.
Mult(1,n);
Выводим номер теста cs. Если n = 1, то перемножать нечего и следует вывести строку "(A1)". Иначе вызываем функцию Print(1, n), которая возвращает строку, содержащую последовательность оптимального произведения матриц.
printf("Case %d: ",cs++); if (n == 1) Answer = "(A1)"; else Answer = Print(1,n);
Выводим результат – строку Answer.
printf("%s\n",Answer.c_str()); }
5. Наибольшая общая подпоследовательность [Вальядолид, 10405]. Пусть f(n, m) – длина максимальной общей подпоследовательности последовательностей x 1 x 2… xn и y 1 y 2… ym. Если x n ¹ y m, то f(n, m) = max(f(n, m - 1), f(n - 1, m)); Если x n = y m, то f(n, m) = 1 + f(n - 1, m - 1); Значения f(n, m) будем хранить в массиве c[0..1000, 0..1000], где c[0, i ] = c[ i, 0] = 0. Каждая следующая строка массива с[ i, j ] вычисляется через предыдущую. Поэтому для нахождения ответа достаточно держать в памяти только две строки длины 1000. Пример. Пусть X = abcdgh, Y = aedfhr. Наибольшей общей подпоследовательностью будет adh, ее длина равна f(6, 6) = 3.
Реализация. Определим функцию max, вычисляющую максимум двух чисел:
int max(int i,int j) { return (i > j)? i: j; }
Массивы x и y содержат входные последовательности, lenx и leny – их длины. Массив m содержит две последние строки динамического преобразования.
char x[1001], y[1001]; int m[2][1001]; int lenx, leny;
Входные данные обрабатываем, пока не встретится конец файла. Читаем две входные последовательности в массивы x и y. При этом значения x[0] и y[0] обнуляем, а входные строки заносим в массивы, начиная с первой ячейки. Длины последовательностей сохраняем в переменных lenx и leny.
x[0] = y[0] = 0; while(gets(x+1),gets(y+1)) { lenx = strlen(x+1); leny = strlen(y+1);
Обнуляем массив m. Динамически вычисляем значения f(i, j). Изначально m [0][ j ] содержит значения f(0, j). Далее в m [1][ j ] заносим значения f(1, j). Поскольку для вычисления f(2, j) достаточно иметь значения двух предыдущих строк массива m, то значения f(2, j) можно сохранять в ячейках m [0][ j ], значения f(3, j) – в ячейках m [1][ j ] и так далее.
memset(m,0,sizeof(m)); for(i = 1; i <= lenx; i++) for(j = 1; j <= leny; j++) if (x[i] == y[j]) m[i % 2][j] = 1 + m[(i-1)%2][j-1]; else m[i % 2][j] = max(m[(i-1)%2][j],m[i%2][j-1]);
В конце алгоритма длина наибольшей общей подпоследовательности будет находиться в ячейке m[ lenx %2][ leny ]. Выводим ее.
printf("%d\n",m[lenx%2][leny]); } 6. Путешествие Теобальдо [Вальядолид, 10681]. Пусть go k [ i ] = 1, если Теобальдо может попасть из начального города s в город i за k переходов, иначе go k [ i ] = 0. Изначально go0[ s ] = 1, go0[ i ] = 0, 1 £ i £ c, i ¹ s. Будем моделировать все возможные переходы Теобальдо, вычисляя значения go k [ i ], 1 £ i £ c, 1 £ k £ d. Очевидно, что go k [ i ] = 1, если существует такое j, что go k -1[ j ] = 1 и существует ребро из города j в город i. Имея все значения go k [ i ] (1 £ i £ c) для некоторого k (0 £ k £ d – 1), вычисляем все значения go k +1[ i ], 1 £ i £ c. Теобальдо может совершить переход из города s в город e за d дней, если go d [ e ] = 1. Пример. Рассмотрим данные первого теста. Теобальдо следует перейти из города s = 3 в город e = 1 за d = 2 дня. Симметрическая матрица переходов m имеет вид: m = Значения go k [ i ] для каждого k - ого перехода приведены в таблице:
Из третьего города за два дня можно перебраться или в первый город, или снова вернуться в третий. Поскольку e = 1, d = 2 и go d [ e ] = go2[1] = 1, то Теобальдо может совершить путешествие. Реализация. Определим максимально возможное число городов MAX = 101. В массиве m содержим матрицу смежности графа, в массивах go и go1 будем пересчитывать значения go k [ i ].
#define MAX 101 int m[MAX][MAX], go[MAX], go1[MAX];
Для каждого теста читаем значения c и l, обнуляем используемые массивы.
while (scanf("%d %d",&c,&l), c + l > 0) { memset(m,0,sizeof(m)); memset(go,0,sizeof(go)); memset(go1,0,sizeof(go1));
Читаем информацию о дорогах между городами, строим матрицу смежности. Дороги двусторонние.
for(i = 0; i < l; i++) { scanf("%d %d",&a,&b); m[a][b] = m[b][a] = 1; }
Вводим данные о маршруте Теобальдо, устанавливаем go[s] = 1.
scanf("%d %d %d",&s,&e,&d); go[s] = 1;
Для каждого k, 1 £ k £ d, совершаем пересчет значений go k [ i ]. Считаем, что go k – 1[ i ] находятся в массиве go, а go k [ i ] кладем в массив go1. Затем копируем массив go1 в массив go и так повторяем процесс d раз.
for(i = 0; i < d; i++) { for(x = 1; x <= c; x++) for(y = 1; y <= c; y++) if (go[y] && m[y][x]) { go1[x] = 1; break;} memcpy(go,go1,sizeof(go)); memset(go1,0,sizeof(go1)); }
В зависимости от значения go[ e ] печатаем результат.
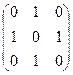
if (go[e]) printf("Yes, Teobaldo can travel.\n"); else printf("No, Teobaldo can not travel.\n"); } 7. Путешествующий торговец [Вальядолид, 10702]. Нумерацию городов буем начинать с 0 (для удобства программирования на Си). Обозначим через d k [ i ] максимальную прибыль, которую может получить торговец, если после совершения k переходов закончит свой путь в городе i (0 £ i < C, города нумеруются от 0 до C - 1). Изначально d0[S] = 0 (нулевая прибыль), d0[ i ] = -1 (прибыль не определена) для i ¹ S. Массив fin[ i ] будет содержать 1, если Джин может завершить свой путь в городе i и 0 иначе. Матрица m[ i, j ] (0 £ i, j < C) будет содержать прибыль, которую можно получить при переходе из города i в j. Торговец должен совершить T переходов. Для каждого перехода будем пересчитывать значения d[ i ]. На k - ом переходе в i - ый город можно попасть из j - ого города (0 £ j < C), при этом максимальная прибыль при достижении i - ого города составит d k [ i ] = Условие d k -1[ j ] ³ 0 гарантирует, что из начального города S за k - 1 переходов можно добраться до города j. Для нахождения результата следует найти максимальное значение среди dT[ i ], для которых fin[ i ] = 1 (город i может быть финальным). Пример. Рассмотрим тест, данный в условии задачи. Поскольку нумерацию городов будем вести с нуля, то начальным городом будет 0, а конечными – 1 или 2. Матрица стоимостей переходов имеет вид: m = Значения d k [ i ] для каждого k - ого перехода приведены в таблице:
Ответом будет max(d2[1], d2[2]) = 7. Реализация. Пока первая строка очередного теста не содержит четыре нуля, читаем входные данные. Заполняем значения массивов d, fin, m. При этом помним, что нумерация городов в тестах начинается с 1, а в массивах будем хранить их с 0.
while(scanf("%d %d %d %d\n",&c,&s,&e,&t), c + s + e + t > 0) { s--; for(i = 0; i < c; i++) {d[i] = -1; fin[i] = 0;} for(d[s] = i = 0; i < c; i++) { for(j = 0; j < c; j++) scanf("%d",&m[i][j]); scanf("\n"); } for(i = 0; i < e; i++) scanf("%d",&j), fin[j-1] = 1; scanf("\n\n");
Для каждого из T переходов динамически пересчитываем оптимальные значения прибыли d[ i ] по выше приведенной формуле. Используем вспомогательный массив d1[ i ].
while (t > 0) { for(i = 0; i < c;i++) { for(d1[i] = j = 0; j < c; j++) { if (d[j] == -1) continue; if (d[j] + m[j][i] > d1[i]) d1[i] = d[j] + m[j][i]; } } memcpy(d,d1,sizeof(d1)); t--; }
Ищем максимальное значение d[ i ], среди тех i, для которых fin[ i ] = 1. Выводим результат.
for(res = i = 0; i < c; i++) if ((d[i] > res) && fin[i]) res = d[i]; printf("%d\n",res); }
8. Трамваи в Барселоне [Вальядолид, 10767]. Построим формулу среднего времени для движения трамвая по одному интервалу. Пусть m – максимально возможная скорость трамвая в начале интервала, s – длина интервала, x – скорость трамвая на ней. Тогда среднее время движения равно f(x) = Найдем скорость x, для которой это время минимально. Раскроим скобки и сгруппируем: f(x) = Производная равна f’(x) = Приравняем ее к нулю, и решим уравнение относительно x. Получим оптимальную скорость x = Пусть a [ i, j ] – время, за которое можно доехать с остановки P i до конца маршрута при условии, что до этого было j поломок. Очевидно, что a [ n, i ] = 0. Обозначим через T0 = a [ i + 1, j ] – оптимальное время, за которое можно доехать с P i +1 до конца с j поломками, T1 = a [ i + 1, j + 1] – оптимальное время, за которое можно доехать с P i +1 до конца с j + 1 поломками. Тогда среднее время проезда от P i до конца равно f(x) = Приравниваем производную к нулю (решаем уравнение f’(x) = 0), вычисляем скорость x, для которой это время будет минимальным. Она равна x = При вычислении a [ i, j ] следует помнить, что до P i было j поломок. Тогда максимально возможная скорость, которую трамвай может выбрать на S i +1, равна m = M0 - j. Если вычисленная оптимальная скорость x будет больше чем M0 - j, то положить x = M0 - j. Оптимальное среднее время, за которое трамвай проедет весь путь, равно a [0, 0]. Вычисление значений массива a идет с конца (сначала вычисляется столбик a [ n - 1, i ] (0 £ i £ n - 1), потом a [ n - 2, i ] (0 £ i £ n - 2) и так далее до a [0, 0]). Каждое значение a [ i, j ] пересчитывается через a [ i + 1, j ] и a [ i + 1, j + 1].
Пример. Рассмотрим второй тест. Данные матрицы a вместе с оптимальными значениями скоростей x приведены в таблице:
Реализация. Читаем входные данные и обнуляем последний столбец матрицы a (a[ n, i ] = 0, 0 £ i £ n).
#include <stdio.h> #include <math.h>
double a[26][26];
void main(void) { int i,j,n; double x,m0,s[26]; while(scanf("%lf %d",&m0,&n) == 2) { for(i=0;i<n;i++) scanf("%lf",&s[i]); for(i=0;i<=n;i++) a[n][i] = 0;
Динамически пересчитываем значения i - го столбца через i + 1 – ый (0 £ i £ n -1). Данные каждого столбца вычисляем сверху вниз, двигаясь от a[ i, 0] до a[ i, i ].
for(i=n-1;i>=0;i--) for(j=0;j<=i;j++) { x = sqrt((m0-j)*s[i]/(10+s[i]/10+a[i+1][j+1]-a[i+1][j])); if (x > m0-j) x = m0-j; a[i][j] = (x/(m0-j))*(s[i]/2/x+10+s[i]/10+a[i+1][j+1]) + (1-x/(m0-j))*(s[i]/x+a[i+1][j]); }
Выводим результат с 4 десятичными знаками после запятой.
printf("%.4lf\n",a[0][0]); } }
9. Распределение оценок [Вальядолид, 10910]. Количество способов, которыми студент может сдать экзамен, равно количеству разложений числа p – n * t на n неотрицательных слагаемых (см. задачу Вальядолид, 10943). Реализация. Определим размер MAX массива m и объявим сам массив m.
#include <stdio.h> #include <memory.h> #define MAX 71
int tests,n,t,p,i,j; int m[MAX][MAX];
Обнуляем массив m. Проведем инициализацию, положив f(i, 1) = f(0, i) = 1 (0 £ i < MAX). Заметим, что f(n, k) = f(n, k – 1) + (f(n – 1, k – 1) + f(n – 2, k – 1) + … f(1, k – 1) + f(0, k – 1)) = f(n, k – 1) + f(n – 1, k) Таким образом, значение m[ i, j ] можно пересчитать как сумму m[ i, j – 1] и m[ i – 1, j ]. Находим значения всех ячеек массива m, совершая таким образом предвычисления.
void main(void) { memset(m,0,sizeof(m)); for(i=0;i<MAX;i++) m[1][i] = m[i][0] = 1; for(i=2;i<MAX;i++) for(j=1;j<MAX;j++) m[i][j] = m[i][j-1] + m[i-1][j];
Читаем количество тестов tests. Для каждого теста вводим значения n, t, p. Положим t = t – n * p. Выводим результат, хранящийся в ячейке m[ n, t ].
scanf("%d",&tests); while(tests--) { scanf("%d %d %d",&n,&t,&p); t -= n*p; printf("%d\n",m[n][t]); } }
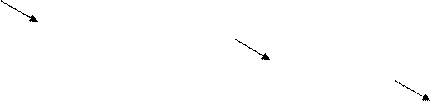
10. Как Вы прибавляете? [Вальядолид, 10943]. Обозначим через f(n, k) количество разбиений числа n на k неотрицательных слагаемых. Если при разбиении числа n на k неотрицательных слагаемых последнее (k - ое) слагаемое равно i (0 £ i £ n), то далее число n – i следует разбить на k – 1 слагаемых, что можно совершить f(n – i, k – 1) способами. Поскольку 0 £ i £ n, то общее число разбиений f(n, k) равно f(n, k – 1) + f(n – 1, k – 1) + f(n – 2, k – 1) + … f(1, k – 1) + f(0, k – 1). Или то же самое что f(n, k) = Очевидно, что f(n, 1) = 1, так как количество способов разбить число n на одно слагаемое равно единице (этим слагаемым будет само число n). Имеет место соотношение f(0, k) = 1, так как единственным разложением числа 0 на k слагаемых будет 0 = 0 + 0 + … + 0 (k раз). Заведем массив m, в котором положим m[ k, n ] = f(n, k), 1 £ k, n £ 100. Индексы массива m и функции f переставлены для удобства программирования: очередная k - ая строка массива m пересчитывается через предыдущую (k – 1) - ую строку. Пример. Для n = 20 и k = 2 существует 21 разбиение: 0 + 20, 1 + 19, 2 + 18,..., 19 + 1, 20 + 0. Для начальных значений n, k таблица m[ k, n ] имеет вид:
|

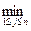 f(i + 1 – vj) + 1, i + 1 ³ vj
f(i + 1 – vj) + 1, i + 1 ³ vj
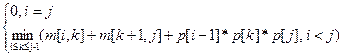
 0
0
 (d k -1[ j ] + m[ j, i ])
(d k -1[ j ] + m[ j, i ])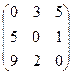
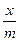
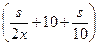 +
+ 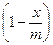

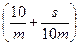 -
- 
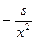 +
+ 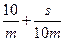
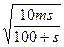
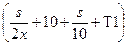 +
+ 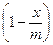
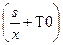
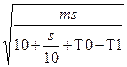
 a[0, 0]
a[0, 0]