Структура простого категорического силлогизма

 

Простым категорическим силлогизмом (сокращенно: ПКС) называется умозаключение, в котором в качестве посылок выступают два категорических суждения. Заключением в нем также является категорическое суждение, в котором содержатся понятия (термины), каждое из которых встречается только в одной посылке. В каждой из посылок имеется еще одно одинаковое для них понятие (термин), которое отсутствует в заключении.

Понятие, общее для обеих посылок, называется средним термином. Понятие, выступающее в роли предиката заключения, именуют большим термином; понятие, которое играет роль субъекта заключения, называют меньшим термином. Больший и меньший термины называют крайними. Больший термин содержит большая посылка, меньший термин содержит меньшая посылка. В стандартно построенном силлогизме большая посылка должна стоять первой.

В силлогизме

1. Все млекопитающие (М) – теплокровные (Р)

(I) 2. Все тюлени (S) – млекопитающие (М)

3. Все тюлени (S) – теплокровные (Р)

понятие «тюлень» – субъект (S) заключения (меньший термин); «теплокровный» – его предикат (Р) (больший термин); «млекопитающие» – средний термин (М); большая посылка – первая, меньшая – вторая.

Силлогистика (учение о силлогизмах) описывает схемы умозаключений, которыми можно пользоваться как правилами вывода. Пример схемы простого силлогизма:

МаР

(II) SаМ

SаР

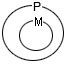
Данная запись является схемой приведенного выше силлогизма (I).

Переход от посылок к заключению в силлогизме связан с ролью среднего термина: отношение субъекта S и предиката Р в заключении опосредуется средним термином М, т.е устанавливается в зависимости от их отношения к среднему терминув посылках. Рассмотрим для примера схему (II). Здесь первая (большая) посылка содержит утверждение о том, что все предметы множества М включаются во множество Р. В свою очередь, вторая (меньшая) посылка указывает, что все предметы множества S включаются во множество М. Графически эти соотношения могут быть представлены так:

 

1. МаР:	2. SаМ:

 

Теперь совместим обе посылки:

 

Хорошо видно, что все предметы множества S оказываются также элементами множества Р, а именно это обстоятельство констатируется в заключении SаР рассматриваемой схемы.

 

Практикум

 

1. Найдите заключение и посылки в следующих силлогизмах:

а) Некоторые морские животные – млекопитающие, ведь все киты – морские животные, и все они – млекопитающие.

б) В каждом квадрате диагонали взаимно перпендикулярны, и поскольку они перпендикулярны в каждом ромбе, все квадраты – ромбы.

*Пример. Ни один скупой человек не счастлив, ибо он вечно не доволен собой, тогда как всякий счастливый человек всегда собой доволен. Суждение Ни один скупой человек не счастлив – это заключение. Далее идет его обоснование, на что указывает союз «ибо». Таким образом: меньшая посылка: Все скупые люди вечно не довольны собой, большая посылка: Всякий счастливый человек всегда собой доволен.

2. Сделайте разбор структуры нижеприведенных ПКС: в каждом из них найдите заключение, затем больший, меньший и средний термины, большую и меньшую посылки. Изобразите отношения между терминами в посылках и заключении с помощью круговых схем.

а) Все рыбы дышат жабрами. Значит, кит – не рыба, ведь он не дышит жабрами.

б) Электрон имеет отрицательный заряд. Электрон – элементарная частица. Следовательно, некоторые элементарные частицы имеют отрицательный заряд.

в) Тополь поглощает углекислоту, ибо тополь – растение, а все растения поглощают углекислоту.

*Пример. Люди грешны. Следовательно, короли грешны, так как они люди. Все суждения в этом умозаключении – общие, хотя явно это не выражено (в естественном языке это допускается). Заключением является стоящее после слова «следовательно» суждение Все короли грешны. Термин «короли» – меньший термин, так как является субъектом S заключения, термин «грешны» – больший термин, поскольку является предикатом Р заключения. Суждение Все люди грешны – большая посылка, потому что содержит предикат Р заключения, а суждение Все короли грешны – меньшая, поскольку содержит субъект S заключения. Средний термин М – «люди», содержащийся в каждой посылке Отношение терминов по их объему таково:

3. Определите, относится ли нижеследующее умозаключение к ПКС:

Кто курит, тот вредит своему здоровью. Значит, среди тех, кто вредит своему здоровью, есть и те, кто курит.