Фигуры и модусы простого категорического силлогизма

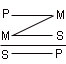
Существует четыре возможных варианта расположения среднего термина в посылках и, соответственно, четыре конструкции или, как их называют, фигуры силлогизма:

1) средний термин является субъектом в большей посылке и предикатом в меньшей (первая фигура);

2) средний термин является предикатом в обеих посылках (вторая фигура);

3) средний термин является субъектом в обеих посылках (третья фигура);

4) средний термин является предикатом в большей посылке и субъектом в меньшей (четвертая фигура).

Названные фигуры схематически изображаются так:

 

1-я фигура	2-я фигура	3-я фигура	4-я фигура

 

Примером умозаключения по первой фигуре может послужить приведенный в разделе 4.2.4.1 вывод (I) (про тюленей). А вот пример умозаключения по второй фигуре:

1. Все юристы (Р) – дипломированные специалисты (М).

2. Некоторые правозащитники (S) не являются дипломированными специалистами (М).

3. Некоторые правозащитники (S) не являются юристами (Р).

Пример умозаключения по третьей фигуре:

1. Все допросы обвиняемого (М) оформляются протоколом (Р).

2. Все допросы обвиняемого (М) – следственные действия (S).

3. Некоторые следственные действия (S) оформляются протоколом (Р).

По четвертой фигуре протекает следующее умозаключение:

1. Все судебные приставы (Р) – чуткие люди (М).

2. Ни один чуткий человек (М) не является злым (S).

3. Ни один злой человек (S) не является судебным приставом (Р).

В каждой фигуре силлогизма возможны варианты – их называют модусами. Модусы фигуры отличаются друг от друга качественной и/или количественной характеристиками входящих в них суждений. Так, модусами первой фигуры являются (среди прочих других) схемы

MaP MеP MaP

SaM SiM SiM

SaP SoPSiP

Количество модусов у каждой фигуры – 64, а всего модусов четырех фигур насчитывается 256. Однако большинство из них не являются правильными, поскольку могут приводить от истинных посылок к ложному заключению. Неправильным, к примеру, является модус первой фигуры:

 

1. Ни один летчик (М) не является незрячим (Р)

2. Некоторые космонавты (S) – летчики (М)

3. Некоторые космонавты (S) – незрячие (Р)

Хотя посылки этого умозаключения – истинные суждения, его заключение ложно.

Для запоминания правильных модусов каждой фигуры в традиционной логике им приписывались соответствующим образом сконструированные названия, указывающие на структуру (строение) модуса. Так, четвертый модус первой фигуры

MeP

SiM

SoP

носит название Ferio. Трем гласным буквам этого слова e, i, o соответствуют типы категорических суждений, входящих в посылки и заключение этого умозаключения. Приведем перечень названий правильных модусов каждой из фигур:

Модусы первой фигуры:	Модусы второй фигуры:
1-й: Barbara (а, а, а) 2-й: Celarent (е,а,е) 3-й: Darii (a, i, i) 4-й: Ferio (е,i,o) 5-й: Barbari (a,а,i) 6-й: Celaront (е,а,o)	e,a,e; a,e,e; e,i,o; a,o,o; e,a,o; a,e,o
Модусы третьей фигуры:
a,a,i; i,a,i; a,i,i; e,a,o; o,a,o; e,i,o
Модусы четвертой фигуры: a,a,i; a,e,e; i,a,i; e,a,o; e,i,o; a,e,o