Дедуктивные выводы из категорических суждений
Приступаем к рассмотрению дедуктивных умозаключений, основанных на внутренней структуре (логической форме) категорических суждений. Рассмотрим первый пример таких умозаключений:
2. Некоторые юристы – депутаты областной думы. Очевидно, что если истинно суждение над чертой, то обязательно истинно суждение под чертой (черта, как и ранее, означает «следовательно»). Так будет и в том случае, если вместо фигурирующих в этом умозаключении понятий (терминов) «депутат областной думы» и «юрист» поставить понятия «студент» и «спортсмен», или «водоплавающие» и «млекопитающие» и т.п. Заменив в этом умозаключении термины на логические переменные S и Р, получим одну из схем (логическую форму) дедуктивного вывода: SiР
В этой схеме выражение SiР является сокращенной записью логической формы частноутвердительного суждения «Некоторые S суть Р», а Рассмотрим второй пример, в котором не одна, а две посылки: 1. Все депутаты областной думы – политические деятели. 2. Некоторые юристы – депутаты областной думы.
Заменив термины этого умозаключения «депутат областной думы», «политический деятель» и «юрист» на логические переменные М, Р и S, получаем схему (логическую форму) дедуктивного вывода МаР SiM
Данная схема составляет логическую основу и таких двухпосылочных умозаключений: Все спортсмены ведут здоровый образ жизни. Некоторые студенты – спортсмены. Следовательно, некоторые студенты ведут здоровый образ жизни .·. Все млекопитающие – теплокровны. Некоторые водоплавающие – млекопитающие. Следовательно, некоторые водоплавающие – теплокровные. Все выводы из категорических суждений делят на два вида: непосредственные и опосредованные. В непосредственных умозаключениях только одна посылка, в опосредованных – две (и более). Рассмотрим в этом разделе однопосылочные выводы из категорических суждений.
4.2.3.1. Выводы по логическому «квадрату» Эти умозаключения основаны на логических отношениях между категорическими суждениями, иллюстрируемых известным нам логическим «квадратом» (раздел 3.3). Напомним, что Рассмотрим разновидности умозаключений, логическим основанием которых является отношение контрадикторности, или противоречия (они называются диагональными). Оно имеет место между общеутвердительным и частноотрицательным суждениями, а также между общеотрицательным и частноутвердительным суждениями(a Отношение логического подчинения (а Осуществляя выводы по логическому квадрату, полезно помнить:
|

 1. Некоторые депутаты областной думы – юристы.
1. Некоторые депутаты областной думы – юристы. РiS
РiS 3. Некоторые юристы – политические деятели.
3. Некоторые юристы – политические деятели. SiP
SiP

 логические отношения не зависят от конкретного содержания суждений, поэтому в дальнейшем эти отношения будут рассматриваться как связи между логическими формами (формулами) суждений. Одно из них – контрарность, или противоположность, имеет место между общеутвердительным и общеотрицательным суждениями (a
логические отношения не зависят от конкретного содержания суждений, поэтому в дальнейшем эти отношения будут рассматриваться как связи между логическими формами (формулами) суждений. Одно из них – контрарность, или противоположность, имеет место между общеутвердительным и общеотрицательным суждениями (a  e). Этот тип отношений характеризуется следующей логической необходимостью: при истинности суждения SаP суждение SeP будет с необходимостью ложным, и наоборот. Поэтому, зная, что Любая кража есть уголовное преступление, заключаем: Неверно, что ни одна кража не является уголовным преступлением. Действительно, при истинности суждения SаР контрарное ему суждение SеР будет обязательно ложным, а его отрицание – истинным. Далее, зная, что Ни один кит не дышит жабрами, заключаем: Неверно, что все киты дышат жабрами. И в том, и в другом случае истинность посылки гарантирует истинность заключения. Остальные два варианта распределения значений истинности контрарных суждений такой логической необходимости не дают.
e). Этот тип отношений характеризуется следующей логической необходимостью: при истинности суждения SаP суждение SeP будет с необходимостью ложным, и наоборот. Поэтому, зная, что Любая кража есть уголовное преступление, заключаем: Неверно, что ни одна кража не является уголовным преступлением. Действительно, при истинности суждения SаР контрарное ему суждение SеР будет обязательно ложным, а его отрицание – истинным. Далее, зная, что Ни один кит не дышит жабрами, заключаем: Неверно, что все киты дышат жабрами. И в том, и в другом случае истинность посылки гарантирует истинность заключения. Остальные два варианта распределения значений истинности контрарных суждений такой логической необходимости не дают.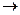 i, e
i, e  о) характеризуется следующей необходимостью: при истинности SaP будет с необходимостью истинно SiP, а при истинности SeP истинным будет SoP. Поэтому зная, что Все свидетели по данному делу прибыли на судебное заседание, заключаем,чтои Некоторые свидетели по данному делу прибыли на судебное заседание. Аналогично, корректным будет переход от посылки Ни один кит не дышит жабрами к заключению Некоторые киты не дышат жабрами.
о) характеризуется следующей необходимостью: при истинности SaP будет с необходимостью истинно SiP, а при истинности SeP истинным будет SoP. Поэтому зная, что Все свидетели по данному делу прибыли на судебное заседание, заключаем,чтои Некоторые свидетели по данному делу прибыли на судебное заседание. Аналогично, корректным будет переход от посылки Ни один кит не дышит жабрами к заключению Некоторые киты не дышат жабрами.


