Разработка математической модели цифровой САР
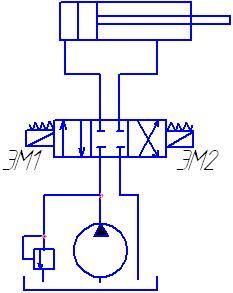
Рассмотрим динамический расчет следящего электрогидравлического привода поступательного действия, упрощенная гидравлическая схема которого представлена на рис.10.
Рис.10. При расчете будем считать, что в насосной станции поддерживается постоянное давление питания Процесс нарастания тягового усилия в ЭМП можно описать следующим уравнением:
где
Постоянную времени
где
Следует также учитывать, что время срабатывания электромагнитов постоянного тока, как правило, почти на порядок больше времени срабатывания электромагнитов, работающих на переменном токе. Для снижения постоянной времени
где Учитывая, что в трехпозиционном ЭГР два электромагнита (ЭМ 1 и ЭМ 2), следует определять суммарное усилие
При этом следует учитывать, что при положительном сигнале рассогласования должен сработать электромагнит ЭМ 1, а при отрицательном – электромагнит ЭМ 2. В последнем случае напряжение питания ЭМП и расчетное усилие Величины давлений на условных входах в ЭГР определятся следующим образом:
Как известно, потери давления
Исходя из последних выражений, можно записать:
Решая последнее уравнение относительно расхода Q, получим:
На основании выражения (4) получим систему уравнений, определяющих расходы
где
В выражениях (5) значения
в котором Величина Исходя из условия неразрывности потока жидкости, записываются уравнения для двух полостей ГЦ:
где
bсi – эквивалентная жесткость гидролинии, определяемая как:
V 0 – неизменяемый объем жидкости в гидролинии; х – перемещение штока ГЦ; Епр – приведенный модуль упругости жидкости, трубопровода и цилиндра:
Еж, Етр, Ец – модули упругости жидкости, стенок трубопровода и цилиндра соответственно; dтр, dц – толщины стенок трубопровода и цилиндра соответственно; dтр, dц – толщины стенок трубопровода и цилиндра соответственно. Далее из уравнения (6) определяются давления нагрузки в обеих полостях ГЦ:
Величина перемещения штока ГЦ определятся из уравнений движения поршня:
где kтр – коэффициент вязкого трения; Fтр – сухое трение поршня и штока; t – удельная сила трения; dп, dш – диаметры поршня и штока; hп, hш – ширина уплотнения на поршне и штоке;
Общая структурная схема привода показана на рис. 11.
Рис.11. Структурная схема гидропривода подъема стрелы. Если качество переходного процесса спроектированного привода не удовлетворяет поставленным требованиям (например, наблюдается значительное перерегулирование и колебательность выходного органа), то можно установить регулятор с дифференциальной составляющей или проектировать систему с подчиненным регулированием по скорости и давлению. В этом случае необходимо устанавливать датчики скорости (расхода) и давления. Однако все это значительно усложняет систему. Добиться приемлемых динамических характеристик можно и путем установки тормозных клапанов. Схема гидропривода с двумя электромагнитными тормозными клапанами ТК показана на рис. 11. Моменты срабатывания тормозных электромагнитов ЭМ3 и ЭМ4 определяются динамическими параметрами привода и определяется условиями:
где При срабатывании ТК жидкость течет через дополнительные гидродроссели ГД. В этом случае в уравнении (5) следует заменить значения турбулентных сопротивлений
Рис.12. Текст программы, описывающей математическую модель гидропривода, представлен ниже:
PROGRAM strela1; USES graph; {-------Global data declarations--------------} CONST ndim=8;n=600; xs:word=60; xm:word=500; ng=3; i:word=0; l=1;m=1;
TYPE mdim=ARRAY[1..ndim] OF REAL; VAR
{ m1:mg;} t,hi,tend,hput,ta,tay:real; a,yd:array[0..m] of real; b,xd:array[0..l] of real; x10,delta1,delta2:real;
y,dery:mdim; dux,Lzad,x,ku,uz1,uz2,uz0,a1,a2,p1,p2,uz11,uz22,xmax,uz1t,uz2t, df,df1,df2,p0,dp1,dp2,q1,q2,bc1,bc2,kq1,kq11,kq22,kq2,ksk,kz,tz,epr, kut,sp1,sp2,Ftr,ktr,mpr,v0,h,Fs,F0,dz,Ftr0,Fa,del,ku1,kreg,ubx,Tet1,Fpr, Uzad,del1,Ubix,La,Beta,fi,gama,teta,Fizad,sin_al,Fimin,Fimax,Gpr, tt1,tt2,kqt1,kqt2,Wstr:REAl; m1,m2,m3,m4,m5,m6,m7:array[0..n+1] OF REAL; my1,my2,my3,my4,my5,my6,my7,max1,max2,max3,max4,max5, max6,max7,mt:REAL; eg,lina, dg:INTEGER; nvp,zz:INTEGER; fdat:text; st1:STRING;
{--------------------------------------------}
FUNCTION sign(x:REAL):REAL; BEGIN IF x>0.0 THEN sign:=1.0 ELSE IF x<0.0 THEN sign:=-1.0 ELSE sign:=0.0 END; { of function sign }
FUNCTION ARCsin(x:REAL):REAL; BEGIN ARCsin:=ARCTAN(x/SQRT(1-SQR(x))) END;
FUNCTION ARCcos(x:REAL):REAL; BEGIN ARCcos:=Pi/2-ARCTAN(x/SQRT(1-SQR(x))) END;
procedure dig; var i,j:integer;pc:real; begin xd[0]:=round(Ubx/delta1);pc:=0; for i:=l downto 1 do begin pc:=pc+b[i]*xd[i];xd[i]:=xd[i-1] end; pc:=pc+b[0]*xd[0]; for i:=m downto 2 do begin pc:=pc-a[i]*yd[i];yd[i]:=yd[i-1] end; pc:=pc-a[1]*yd[1];yd[1]:=pc;yd[0]:=pc; Ubix:=delta2*round(yd[0]) end;
PROCEDURE outp; BEGIN IF i mod 5=0 THEN WRITELN(‘t=’,t:5:3,’ V=’,y[5]:8:4, ‘ Wstr=’,Wstr:8:5, ‘ dL=’,(Lzad-y[6]):8:5, ‘ Fi=’,Fi*180/Pi:8:4,’ F0=’,F0:8:2);
WRITELN(fdat,’ ‘,t:5:3,’ ‘,y[5]:8:4, ‘ ‘,Wstr:8:5, ‘ ‘,y[3]:10:2,’ ‘,y[4]:10:2, ‘ ‘,(Lzad-y[6]):8:5, ‘ ‘,Fi*180/Pi:8:4,’ ‘,F0:8:2);
m1[i]:=y[3];{давление в поршневой полости} m2[i]:=y[4];{давление в штокой полости} m3[i]:=y[5];{скорость штока} m4[i]:=y[6];{перемещение штока} m5[i]:=uz1t; m6[i]:=uz2t; m7[i]:=ubix{uz1};
i:=i+1 END; { of procedure outp }
procedure fct; BEGIN
IF nvp=0 THEN BEGIN uz11:=0;uz22:=0 END; if y[3]<0 then y[3]:=0; if y[4]<0 then y[4]:=0; dux:=Ubix; {=(Lzad-y[6])*ku;} IF dux>=a1 THEN uz1:=uz0 ELSE IF dux<=a2 THEN uz1:=0 ELSE uz1:=uz11; IF dux<=-a1 THEN uz2:=-uz0 ELSE IF dux>=-a2 THEN uz2:=0 ELSE uz2:=uz22; dery[1]:=(kz*uz1-y[1])/tz; dery[2]:=(kz*uz2-y[2])/tz; df:=y[1]+y[2];
IF df>=df1 THEN BEGIN p1:=p0; p2:=0; zz:=1 END ELSE IF df<=-df1 THEN BEGIN p1:=0; p2:=p0; zz:=1 END ELSE BEGIN p1:=0; p2:=0; zz:=0 END;
dp1:=p1-y[3]; dp2:=p2-y[4];
IF ABS(Lzad-y[6])<=dz THEN IF uz1=uz0 THEN BEGIN uz1t:=uz0; uz2t:=0 END ELSE IF uz2=-uz0 THEN BEGIN uz2t:=uz0; uz1t:=0 END ELSE BEGIN uz1t:=uz0;uz2t:=uz0 END ELSE BEGIN uz1t:=0; uz2t:=0 END;
dery[7]:=(kz*uz1t-y[7])/tt1; IF y[7]>=df1 THEN kq1:=kqt1 ELSE kq1:=kq11; dery[8]:=(kz*uz2t-y[8])/tt2; IF y[8]>=df1 THEN kq2:=kqt2 ELSE kq2:=kq22;
q1:=(SQRT(SQR(ksk)+4*kq1*ABS(dp1))-ksk)*0.5/kq1*SIGN(dp1)*zz; q2:=(SQRT(SQR(ksk)+4*kq2*ABS(dp2))-ksk)*0.5/kq2*SIGN(dp2)*zz; bc1:=(v0+sp1*y[6])/epr; bc2:=(v0+sp2*(xmax-y[6]))/epr; dery[3]:=(q1-sp1*y[5]-kut*y[3])/bc1; dery[4]:=(q2+sp2*y[5]-kut*y[4])/bc2; {Определение угла Fi:} sin_al:=1-y[6]*y[6]/2/La/La; Fi:=(-beta+oole(sin_al)); {Определение нагрузки на шток:} Gama:=Fi+ARCcos(y[6]/2/La); F0:=Gpr*sin(Gama);
Fa:=y[3]*sp1-y[4]*sp2-F0; IF y[5]=0 THEN IF ABS(Fa)>Ftr0 THEN Ftr:=Ftr0*sign(Fa) ELSE Ftr:=Fa ELSE Ftr:=Ftr0*sign(y[5]); dery[5]:=(Fa-Ftr-y[5]*ktr)/mpr; dery[6]:=y[5]; Uzad:=(Lzad)*ku1; Ubx:=Uzad-y[6]*ku1; {Определение угловой скорости стрелы:} Wstr:=La*y[5]*sin(Gama-Fi);
If nvp=2 THEN BEGIN uz11:=uz1;uz22:=uz2;
END; END; { of procedure fct }
procedure rkgsd; label 1,2,3; type m=array[1..4] of real;
const a:m=(1/6,1/3,1/3,1/6); b:m=(0.5,0.5,1.0,1.0); var y1,y2:mdim; pz,pv:array[1..ndim] of oolean; signz:array[1..ndim] of shortint; r,aj,bj,ht,h1,tput,tta:real; ita,iput,iend:oolean; i,j:integer;
function sign(x:real):shortint; begin if x>0 then sign:=1 else if x<0 then sign:=-1 else sign:=0 end;
procedure p1; var i:word; begin for i:=1 to ndim do begin if pv[i] then begin y[i]:=0; pv[i]:=false end; pz[i]:=true end end;
procedure p2; var signv:shortint; i:word; begin for i:=1 to ndim do begin signv:=sign(y[i]); if not pv[i] then if signv<>0 then if pz[i] then begin signz[i]:=signv;pz[i]:=false end else if signv<>signz[i] then pv[i]:=true end end;
begin for i:=1 to ndim do begin pv[i]:=false;pz[i]:=true end;
tput:=t;tta:=t+ta; fct; iend:=false;ita:=false; 1:iput:=false;outp;tput:=tput+hput; 2: if ita then begin ita:=false;dig;tta:=tta+ta end; ht:=h; y1:=y;y2:=y; h1:=tput-t; if h1<=h then begin ht:=h1; iput:=true end; h1:=tta-t; if h1<=ht then begin ht:=h1; iput:=false;ita:=true end; h1:=tend-t; if h1<=ht then begin if h1<ht then begin ht:=h1;iput:=false end; iend:=true end; j:=1; 3: aj:=a[j]; bj:=b[j]; for i:=1 to ndim do begin r:=dery[i]*ht; y2[i]:=y2[i]+aj*r; if j<>4 then y[i]:=y1[i]+bj*r; end; if j<>4 then begin
j:=j+1; if j<>3 then t:=t+0.5*ht; p2; fct; goto 3 end; y:=y2;p1; p2; fct; if iend then begin outp;exit end; if iput then goto 1; goto 2 end; {----------------------------------------------} BEGIN { main program } {---------Initialization----------------} {Параметры реле:} a1:=1;a2:=0.8*a1;del:=0.00025{точность в м}; ku:=1/del; ku1:=1000; {Параметры П-регулятора:}kreg:=1/ku1/del; {Геометрические параметры крепления гидроцилиндра:} La:=0.5; Beta:=65*Pi/180; {Заданные параметры системы:} Fimin:=0*Pi/180; Fimax:=85*Pi/180;Fizad:=25*Pi/180; {Параметры основного ЭМП:} df1:=160;kz:=180/220;uz0:=220; tz:=0.05; {Постоянные времени тормозных ЭМП:} tt1:=0.02;tt2:=0.02;
{Давление настройки гидросистемы:}p0:=1.6e7; ksk:=7.8e8; dz:=0.016 {настройка расстояния торможения}; kq11:=20e13;kq22:=20e13;{для регулировки скорости} {Параметры гидросистемы:} mpr:=50{приведенная масса нагрузки}; kqt2:=8.2e18; kqt1:=8.2e18{тормозные дроссели}; v0:=22.5e-5;sp1:=0.005;sp2:=0.0045;xmax:=2.0;{параметры гидроцилиндра} epr:=1.6e8; kut:=20e-18;ktr:=2.5e5;Ftr0:=100; Gpr:=35e3;{приведенная вертикальная нагрузка} {Заданные значения цифовой части} {ubx:=0;} delta1:=0.2; delta2:=0.2;{цены младших разрядов АЦП и ЦАП} Ta:=0.05;{период дискретизации}TAY:=0;{время запаздывания} {Параметры цифрового регулятора:}B[0]:=kreg;B[1]:=0;A[0]:=1;A[1]:=0; FOR i:=1 TO 5 DO y[i]:=0; y[6]:=La*SQRT(2*(1-cos(Fimin+Beta)));{нач условие для перемещения} y[7]:=0; y[8]:=0;
{Расчет заданного перемещения гидроцилиндра:} Lzad:=La*SQRT(2*(1-cos(Fizad+Beta)));
h:=0.0001; tend:=20; t:=0; hput:=tend/n; assign(fdat,’rez_priv_n.txt’);rewrite(fdat); WRITELN(fdat,’ t ‘,’ V ‘,’ Wstr ‘, ‘ p_1 ‘,’ p_2 ‘,’ dL’,’ Fi’,’ F0 ‘); i:=0; rkgsd;close(fdat); eg:=0; initgraph(eg,dg,’c:\tp_7_1\bgi’); IF graphResult<>0 THEN BEGIN WRITELN(' Графика не открыта'); READLN; halt END; lina:=getmaxy div 2; {провести нулевую линию по середине экрана} mt:=xm/n; {масштаб по времени} {выбор масштаба для m1} max1:=ABS(m1[0]); FOR i:=1 TO n DO IF ABS(m1[i])>max1 THEN max1:=ABS(m1[i]); IF max1<>0 THEN my1:=(lina-20)/max1 ELSE my1:=1;
{выбор масштаба для m2} max2:=ABS(m2[0]); FOR i:=1 TO n DO IF ABS(m2[i])>max2 THEN max2:=ABS(m2[i]); IF max2<>0 THEN my2:=(lina-40)/max2 ELSE my2:=1; { my2:=my1;}
{выбор масштаба для m3} max3:=ABS(m3[0]); FOR i:=1 TO n DO IF ABS(m3[i])>max3 THEN max3:=ABS(m3[i]); IF max3<>0 THEN my3:=(lina-60)/max3 ELSE my3:=1;
{выбор масштаба для m4} max4:=ABS(m4[0]); FOR i:=1 TO n DO IF ABS(m4[i])>max4 THEN max4:=ABS(m4[i]); IF max4<>0 THEN my4:=(lina-80)/max4 ELSE my4:=1;
{выбор масштаба для m5} max5:=ABS(m5[0]); FOR i:=1 TO n DO IF ABS(m5[i])>max5 THEN max5:=ABS(m5[i]); IF max5<>0 THEN my5:=(lina-20)/max5 ELSE my5:=1;
{выбор масштаба для m6} max6:=ABS(m6[0]); FOR i:=1 TO n DO IF ABS(m6[i])>max6 THEN max6:=ABS(m6[i]); IF max6<>0 THEN my6:=(lina-20)/max6 ELSE my6:=1;
{выбор масштаба для m7} max7:=ABS(m7[0]); FOR i:=1 TO n DO IF ABS(m7[i])>max7 THEN max7:=ABS(m7[i]); IF max7<>0 THEN my7:=(lina-20)/max7 ELSE my7:=1; if my6>my7 then my6:=my7 else my7:=my6;
setlinestyle(1,0,1); line(xs,lina,xs+xm,lina); outtextxy(xs-15,lina-4,’0’); FOR i:=0 TO n DO IF i mod (n div 5)=0 THEN BEGIN line(xs+round(mt*i),20,xs+round(mt*i),2*lina-20); str(i/n*tend:3:1,st1); outtextxy(xs+round(mt*i)-12,2*lina-15,st1) END; setlinestyle(0,0,1);
setcolor(4); str(max1:10:1,st1); outtextxy(0,0,st1); moveto(xs,lina-round(my1*m1[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my1*m1[i]));
setcolor(5); str(max2:10:1,st1); outtextxy(0,10,st1); moveto(xs,lina-round(my2*m2[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my2*m2[i]));
setcolor(BLUE);str(max3:6:5,st1); outtextxy(0,20,st1); moveto(xs,lina-round(my3*m3[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my3*m3[i]));
setcolor(GREEN); str(max4:6:4,st1); outtextxy(0,40,st1); moveto(xs,lina-round(my4*m4[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my4*m4[i]));
setcolor(11); str(max5:6:2,st1); outtextxy(0,60,st1); moveto(xs,lina-round(my5*m5[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my5*m5[i]));
setcolor(12); str(max6:6:2,st1); outtextxy(0,80,st1); moveto(xs,lina-round(my6*m6[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my6*m6[i]));
setcolor(13); str(max7:6:2,st1); outtextxy(0,100,st1); moveto(xs,lina-round(my7*m7[0])); FOR i:=1 TO n DO lineto(xs+round(mt*i),lina-round(my7*m7[i])); readln; END. { end of main program }
Результаты моделирования представлены ниже в виде графиков на рис.13-19.
Рис.13. Зависимость V(t).
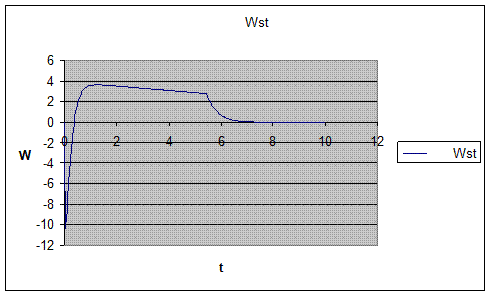
Рис.14. Зависимость w(t).
Рис.15. Зависимость p1(t).
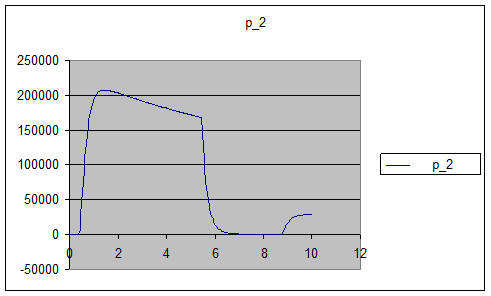
Рис.16. Зависимость p2(t).
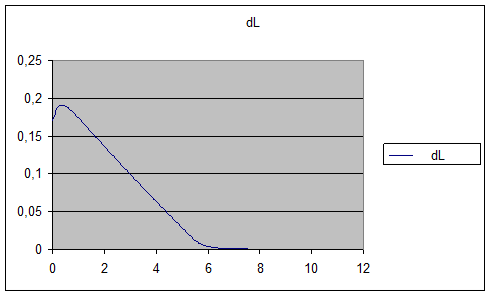
Рис.6. Изменение длинны L в зависимости от времени.
Рис.18. Изменение угла поворота стрелы φ от времени.
Рис.19. Изменение нагрузки на штоке гидроцилиндра от времени. Также представлены результаты моделирования гидросхемы, изображенной на рис.10. в программе Hydrocad. Также представлены математические модели гидроаппаратов. Ниже на рис.20-23 представлены графики полученные в результате моделирования данной гидросхемы:
Рис.6. Расход в поршневой полости гидроцилиндра.
Рис.21. Давление в поршневой полости гидроцилиндра.
Рис.22. Скорость поршня гидроцилиндра.
Рис23. Перемещение поршня гидроцилиндра.
Математические модели аппаратов гидросистемы: Насос: procedure NEWMATHMODEL( Const P1 {Входной трубопровод: Давление, Па}, P2 {Сливной трубопровод: Давление, Па}, P_nom {Давление номинальное, МПа}, q_nas {Рабочий объём номинальный, см3/об}, n_nom {Частота вращения номинальная, об/мин}, kpd_o_nom {КПД обьемный при номинальном режиме работы, } : TFloat; Var Q1 {Входной трубопровод: Расход, м3/сек}, Q2 {Сливной трубопровод: Расход, м3/сек} : TFloat); begin Q1:=q_nas/1e6*n_nom/60; Q2:=Q1-Q1*((1-kpd_o_nom)*(P2/P_nom/1e6)); end; Распределитель: rocedure RASPR_4X3_II( Const P1 {Входной трубопровод: Давление, Па}, P2 {Трубопровод № 2: Давление, Па}, P3 {Трубопровод № 3: Давление, Па}, P4 {Трубопровод № 4: Давление, Па}, d_usl {Диаметр условного прохода, м.}, Pos {Позиция распределителя, } : TFloat; Var Q1 {Входной трубопровод: Расход, м3/сек}, Q2 {Трубопровод № 2: Расход, м3/сек}, Q3 {Трубопровод № 3: Расход, м3/сек}, Q4 {Трубопровод № 4: Расход, м3/сек} : TFloat); var f: TFloat; begin f:=pi*sqr(D_usl)/4; if Pos=0 then begin Q2:=0; Q3:=0; Q1:=0.7*f*Sqrt(2/Ro*(Abs(P1-P4)))*Sign(P1-P4); Q4:=Q1; end; if Pos=1 then begin Q1:=0.7*f*Sqrt(2/Ro*(Abs(P1-P2)))*Sign(P1-P2); Q2:=Q1; Q3:=0.7*f*Sqrt(2/Ro*(Abs(P4-P3)))*Sign(P4-P3); Q4:=-Q3; end; if pos=2 then begin Q1:=0.7*f*Sqrt(2/Ro*(Abs(P1-P3)))*Sign(P1-P3); Q3:=Q1; Q2:=0.7*f*Sqrt(2/Ro*(Abs(P4-P2)))*Sign(P4-P2); Q4:=-Q2; end; end; Предохранительный клапан: procedure PRED_KLAP( Const P1 {Входной трубопровод: Давление, Па}, P2 {Трубопровод № 2: Давление, Па}, d_usl {Диаметр условного прохода, м.}, Pnastr {Давление настройки, МПа} : TFloat; Var Q1 {Входной трубопровод: Расход, м3/сек}, Q2 {Трубопровод № 2: Расход, м3/сек} : TFloat); begin if (P1 > Pnastr * 1e6) then Q1:= 0.7 * pi* Sqr(d_usl) / 4 * Sqrt(2/Ro * Abs(P1-P2)) * Sign(P1-P2) else Q1:= 0; Q2:= Q1; end; Гидроцилиндр: procedure GC_1_BASE( Const P1 {Входной трубопровод: Давление, Па}, P2 {Сливной трубопровод: Давление, Па}, F1 {Поршень: Усилие, Н}, V1 {Поршень: Скорость, м/сек}, X1 {Поршень: Перемещение, м}, L_cil {Ход поршня, мм.}, d_por {Диаметр поршня, мм.}, d_st {Диаметр штока, мм.}, F_tr {Сила страгивания (сухого трения), }, K_per {Коэффициент перетечек между полостями, }, Lam {Коэффициент вязкого трения, }, m_cil {Приведённая масса, } : TFloat; Var Q1 {Входной трубопровод: Расход, м3/сек}, Q2 {Сливной трубопровод: Расход, м3/сек}, dV1 {Поршень: Приращение скорости, м/сек}, dX1 {Поршень: Приращение перемещения, м} : TFloat); Var f_por, f_st, F_upora, F_tr1: Single; begin F_upora:= 0; if X1 < 0 then F_upora:= Estal * X1; if X1 > L_cil/1000 then F_upora:= Estal * (X1 - L_cil/1000); f_por:= pi * Sqr(d_por/1000) / 4; f_st:= pi * (Sqr(d_por/1000) - Sqr(d_st/1000)) / 4; F_tr1:=0; F_tr1:=F_tr; if ((F_tr1> (P1*f_por-P2*f_st-F_upora-Lam*V1-0.02*F1*sign(V1)-F1)) and (V1=0)) then F_tr1:=(P1*f_por-P2*f_st-F_upora-Lam*V1-0.02*F1*sign(V1)-F1); {движущая сила меньше силы страгивания} dV1:= 1/m_cil * (P1 * f_por - P2 * f_st - F_upora - Lam*V1 - 0.02*F1*sign(V1) - F_tr1*Sign(V1) - F1); dX1:= V1; Q1:= V1 * f_por + K_per*(P1-P2)*Sign(P1-P2); Q2:= V1 * f_st + K_per*(P1-P2)*Sign(P1-P2); end;
Литература. 1. Усов.А.А, Свешников.ВК. Станочный гидропривод. М. Машиностроение. 1968г. 2. Бутов.А.И. Расчет объемного гидропривода. Методическое указание к курсовому проектированию. Новочеркасск. 1997 г. 3. Анурьев.В.И. Справочник конструктора-машиностроителя. М. Машиностроение. 1992 г.
* Толщина стенок сливного и всасывающего трубопроводов увеличена из условий жесткости и соответствует стандартному ряду. * САР - система автоматического регулирования.
|

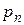 , давление на сливе равно
, давление на сливе равно  . Верхний предел давления ограничивается работой предохранительного клапана ПК. Реверс работы исполнительного гидродвигателя ГЦ осуществляется за счет трехпозиционного электрогидрораспределителя ЭГР. При использовании электрогидрораспределителей время их переключения из нейтрального положения в одно из рабочих, приведенное в паспорте, распределяется примерно в следующем соотношении: (80 – 85) % уходит на процесс нарастания тока и тягового усилия в электромагнитной системе, а остальное время – на движение золотника. Поэтому при анализе динамических характеристик привода можно рассчитывать процесс нарастания усилия в электромеханическом преобразователе (ЭМП) ЭГР, считая при этом, что само смещение золотника осуществляется мгновенно. В этом случае значение площади проходного сечения ЭГР принимает только два значения:
. Верхний предел давления ограничивается работой предохранительного клапана ПК. Реверс работы исполнительного гидродвигателя ГЦ осуществляется за счет трехпозиционного электрогидрораспределителя ЭГР. При использовании электрогидрораспределителей время их переключения из нейтрального положения в одно из рабочих, приведенное в паспорте, распределяется примерно в следующем соотношении: (80 – 85) % уходит на процесс нарастания тока и тягового усилия в электромагнитной системе, а остальное время – на движение золотника. Поэтому при анализе динамических характеристик привода можно рассчитывать процесс нарастания усилия в электромеханическом преобразователе (ЭМП) ЭГР, считая при этом, что само смещение золотника осуществляется мгновенно. В этом случае значение площади проходного сечения ЭГР принимает только два значения:  и
и  .
. ,
, – тяговое усилие на одном из двух электромагнитов ЭМ 1 или ЭМ 2;
– тяговое усилие на одном из двух электромагнитов ЭМ 1 или ЭМ 2;  – напряжение питания электромагнитов, определяемое в общем случае как
– напряжение питания электромагнитов, определяемое в общем случае как 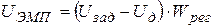 ((
(( ) – сигнал рассогласования,
) – сигнал рассогласования,  – передаточная функция регулятора);
– передаточная функция регулятора);  – коэффициент усиления (преобразования) ЭМП, который можно определить из технической характеристики на ЭГР как
– коэффициент усиления (преобразования) ЭМП, который можно определить из технической характеристики на ЭГР как ,
, – номинальное тяговое усилие электромагнита (из технической характеристики).
– номинальное тяговое усилие электромагнита (из технической характеристики).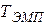 можно определить, исходя из общего решения дифференциального уравнения (1):
можно определить, исходя из общего решения дифференциального уравнения (1): ,
, – время срабатывания (переключения) ЭГР (из технической характеристики), и соотношения (2). Тогда получим:
– время срабатывания (переключения) ЭГР (из технической характеристики), и соотношения (2). Тогда получим: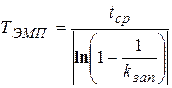 .
. ,
, – желаемая постоянная времени ЭМП.
– желаемая постоянная времени ЭМП.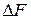 от действия двух ЭМП:
от действия двух ЭМП: .
. принимают также отрицательные значения.
принимают также отрицательные значения.

 складываются из потерь при ламинарном режиме течения жидкости
складываются из потерь при ламинарном режиме течения жидкости  , зависящих от протяженности гладких гидролиний, и турбулентном режиме
, зависящих от протяженности гладких гидролиний, и турбулентном режиме  , наблюдаемом при течении жидкости через различные сопротивления. Учитывая, что расход в любом сечении один и тот же, можно записать:
, наблюдаемом при течении жидкости через различные сопротивления. Учитывая, что расход в любом сечении один и тот же, можно записать: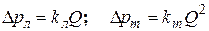 .
.
 .
.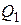 и
и  поршневой и штоковой магистралей ГЦ:
поршневой и штоковой магистралей ГЦ:
 – функция положения золотника ЭГР, определяемая как
– функция положения золотника ЭГР, определяемая как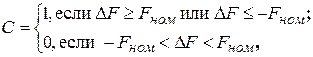
 – суммарные потери давления в магистрали, определяемые как
– суммарные потери давления в магистрали, определяемые как ,
, – давление нагрузки в поршневой или штоковой полостях ГЦ.
– давление нагрузки в поршневой или штоковой полостях ГЦ. можно оценить из уравнения Пуазейля:
можно оценить из уравнения Пуазейля: ,
, – протяженность гидролинии, n и r ж – кинематическая вязкость и плотность рабочей жидкости,
– протяженность гидролинии, n и r ж – кинематическая вязкость и плотность рабочей жидкости,  – внутренний диаметр гидролинии.
– внутренний диаметр гидролинии. , включающая в себя все турбулентные сопротивления, в том числе и дроссели для регулирования скорости потока, определяет скорость движения выходного звена или рабочего органа. Ее значение определяется на основании требований к скорости и быстродействию привода.
, включающая в себя все турбулентные сопротивления, в том числе и дроссели для регулирования скорости потока, определяет скорость движения выходного звена или рабочего органа. Ее значение определяется на основании требований к скорости и быстродействию привода.
 и
и  – площади поршневой и штоковой полостей ГЦ:
– площади поршневой и штоковой полостей ГЦ: ;
;  ,
,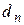 – диаметр поршня,
– диаметр поршня, 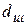 – диаметр штока;
– диаметр штока; – коэффициент утечек и перетечек, определяемый ориентировочно из условия, что расход на утечки
– коэффициент утечек и перетечек, определяемый ориентировочно из условия, что расход на утечки  не должен превышать 5 % расхода, идущего на перемещение штока, определяемого исходя из требования к быстродействию привода:
не должен превышать 5 % расхода, идущего на перемещение штока, определяемого исходя из требования к быстродействию привода: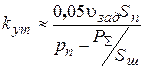 ,
, – заданная или требуемая скорость перемещения штока ГЦ,
– заданная или требуемая скорость перемещения штока ГЦ,  – сумма приложенных к выходному звену привода активных сил;
– сумма приложенных к выходному звену привода активных сил; ,
,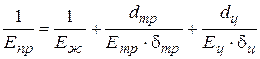 ,
,
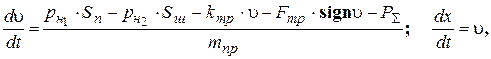


 – напряжение питания электромагнитов ЭМ3 и ЭМ4;
– напряжение питания электромагнитов ЭМ3 и ЭМ4;  – расстояние, на котором происходит срабатывание тормозных клапанов.
– расстояние, на котором происходит срабатывание тормозных клапанов.