Движение материальной точки по окружности. Угол поворота, угловая скорость и угловое ускорение.
Движение материальной точки по окружности – особый частный случай движения вообще, о котором говорилось выше. Его математическое описание существенно упрощается благодаря тому, что для определения местоположения точки на окружности достаточно всего одной координаты. Особенно важно, что такое движение широко распространено в природе. Например, движение почти всех планет Солнечной системы происходит по орбитам, весьма близким по форме к круговым. Поместим начало координат (тело отсчета) в центр окружности, и пусть радиус-вектор точки в начальный момент времени был Изменение угла поворота называется угловым перемещением:
Быстрота углового перемещения называется угловой скоростью:
Размерность угловой скорости – рад/с. Быстрота изменения угловой скорости называется угловым ускорением:
Размерность углового ускорения – рад/с2. Движение по окружности – всегда ускоренное. Ведь скорость имеет не только величину (модуль), но и направление. Даже если скорость v постоянна по величине, то имеется ускорение, направленное к центру окружности и отвечающее за изменение направления скорости. Эту составляющую полного ускорения называют нормальной, она в любой момент времени равна an = v2/R = ω2R.
|

 , а в конечный -
, а в конечный - 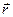 . Тогда угол j между векторами
. Тогда угол j между векторами 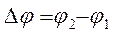 .
. – средняя угловая скорость;
– средняя угловая скорость;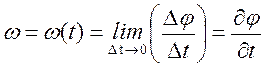 – мгновенная угловая скорость.
– мгновенная угловая скорость. – среднее угловое ускорение;
– среднее угловое ускорение; – мгновенное угловое ускорение.
– мгновенное угловое ускорение.


