Средняя и мгновенная скорости. Ускорение.Если за время Dt тело совершило перемещение
Скорость, таким образом, характеризует быстроту перемещения. При нахождении средней скорости и время, и перемещение могут быть сколь угодно большими. Можно говорить и о средней скорости на пути
Очевидно, что
Будем уменьшать промежуток времени:
при этом В пределе при
производная радиус-вектора по времени. Если скорость постоянна, то такое движение называют равномерным. Однако в общем случае скорость зависит от времени. Быстроту изменения скорости характеризует ускорение:
В пределе при Dt ® 0 получим мгновенное ускорение, т.е. ускорение тела в момент времени:
производная скорости по времени или вторая производная радиус-вектора по времени. Движение с постоянным ускорением называют равнопеременным (равноускоренным или равнозамедленным), но в общем случае ускорение зависит от времени. Итак, зная кинематические уравнения движения тела, можно определить его скорость и ускорение в любой момент времени, т.е. полностью описать движение. Верно и обратное: зная зависимость ускорения от времени и начальные условия (скорость и радиус-вектор в начальный момент времени), можно получить уравнение движения тела. Действительно, если
|
, то говорят, что оно двигалось со средней скоростью
.
:
.
.
,
.
-
-
, 
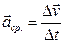
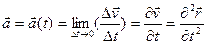, то
,
.
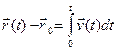