Связь между линейными и угловыми кинематическими характеристиками движения.
Прямолинейное движение и движение по окружности описываются с помощью одинакового математического аппарата. Это говорит о внутреннем сходстве, единстве этих движений. Количественные характеристики прямолинейного и вращательного движений связаны между собой простыми соотношениями. Рассмотрим малый угол поворота
где R – радиус окружности. Это соотношение справедливо и для любых путей, пройденных точкой по окружности:
например, Поскольку радиус окружности – величина постоянная, то, взяв производную левой и правой частей соотношения (*) по времени, получим, что
a = R e. Таким образом, методы классической кинематики позволяют описывать как поступательное, так и вращательное движение макроскопического тела, т.е. всякое его сложное движение, которое может быть представлено как сочетание поступательного и вращательного. Для того, чтобы определить положение тела в любой момент времени, надо знать начальные условия и ускорения. Ускорения же обусловлены взаимодействием тела с другими телами, и их нахождением занимается другой раздел механики – динамика.
Лекция 4. Силы в природе. Фундаментальные взаимодействия.
|
. Ему соответствует малое перемещение 
, 
- длине дуги окружности, т.е. пути точки по окружности.
, (*)
,
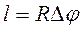, 2π– полный поворот точки вокруг центра окружности.
,
