Теорема Гаусса-Маркова
Љ®§Ґ«мбЄ – ЋЇвЁ Џгбвлм – Ќ.ЏалбЄЁ -?®а¤Ё® 05.09, 12.09, 19.09, 26.09 ‘Ў®а ў 06:45. ЋвЇаў«ҐЁҐ ў 07:00 „®а®Ј ўҐ¤св ў Єап, Є®в®алҐ гЇ®пгвл Ґйс г аЁбЄЁе Ёбв®аЁЄ®ў, ЄЄ §Ґ«Ё б«ўп -ўпвЁзҐ©. Ѓгап Ёбв®аЁп Ў®амЎл § нвЁ Ў®ЈвлҐ §Ґ«Ё зЁҐвбп б 9-Ј® ўҐЄ Ё Ґ б«гз©® нв®© Љ«г¦бЄ®© §Ґ«Ґ б®Ўал ¤аҐўҐ©иЁҐ б«ўпбЄЁҐ Ї®бҐ«ҐЁп - ЄаҐЇ®бвЁ: Ѓ®а®ўбЄ, ђл«мбЄ, Ћ¤®Ґў, Љ®§Ґ«мбЄ, ®ЈЁҐ Ё§ Є®в®але бв«Ё ¤ге®ўлЁ жҐваЁ ¤аҐўҐ© ђгбЁ. Љ®§Ґ«мбЄ - ¤аҐўҐ©иЁ© Ј®а®¤ ўпвЁзҐ©, ®вў¦ле Ё еЁвале ў®Ё®ў, ў вҐзҐЁҐ ®ЈЁе ўҐЄ®ў §йЁйўиЁе бў®Ё §Ґ«Ё ®Ј®«о¤® ЇгвЁ Ґ¦¤г „ҐЇа® Ё ‚®«Ј®©, Ґ¦¤г б«ўпбЄЁ Ё гбг«мбЄЁЁ ЁаЁ. ‡вҐ нвЁ Ґбв бв®ўпвбп ЇгвЁ о¦ле Є®зҐўЁЄ®ў ў Ёе ЎҐЈе ᥢҐаго ђгбм. ЌҐ ҐҐҐ 6-вЁ а§ Ј®а®¤ б¦ЁЈ«бп ¤®в«, Љ®§Ґ«мбЄ Ґ¤ЁбвўҐл© Ё§ агббЄЁе Ј®а®¤®ў Ў®«миҐ Ґбпж ¤Ґа¦«бп Їа®вЁў е Ѓвлп, бвў ЇҐаўл ®вҐзҐб⢥л бЁў®«® 㦥бвў Ё ў®«Ё. ќЄбЄгабЁп ў ‘ўпв®-‚ўҐ¤ҐбЄЁ© Љ®§Ґ«мбЄЁ© г¦бЄ®© ®бвлам, ЋЇвЁг Їгбвлм: аеЁвҐЄвгал© бЎ«м ®бвлап, Ї®бҐйҐЁҐ ‚ўҐ¤ҐбЄ®Ј®, Љ§бЄ®Ј®, ‚«¤ЁЁабЄ®Ј® еа®ў, Ј¤Ґ Ї®Є®пвбп бўпвлҐ ®йЁ ЋЇвЁбЄЁе бва楢. Џ®бҐйҐЁҐ €®®-ЏаҐ¤вҐзҐбЄ®Ј® бЄЁв, ЄҐ«мЁ Ё ®бўпйс®Ј® Є®«®¤ж бў. Ђўа®бЁп ЋЇвЁбЄ®Ј®. ЊЁа еа®ў Ё ®бвл३ б®ўҐа襮 ®б®Ўл©. ‡¤Ґбм Ѓ®Ј ўбваҐзҐв 祫®ўҐЄ, 祫®ўҐЄ ў®§ўайҐвбп Є б®г ᥡҐ. ЋЁ ў®§ЁЄов ў бле гЁЄ«мле Ё ЇаҐЄабле гЈ®«Єе §Ґ«Ё, Ё ЇаҐ¤бвў«пов б®Ў®© б®ЎаЁҐ 襤Ґўа®ў Єаб®вл Ё еаЁ«ЁйҐ бўпвлм. "‘ЇбҐЁҐ ђ®ббЁЁ зсвбп б ®иҐбЄ®© ЄҐ«мЁ" - вЄ бЄ§«„®б⮥ўбЄЁ©, Ї®бҐвЁў ЋЇвЁг Їгбвлм. €Ґ® §¤Ґбм, ў ЋЇвЁҐ, Ј«ў®© ¤ге®ў®© ва¤ЁжЁҐ©, бвҐа¦Ґ ўбҐ© ®иҐбЄ®© ¦Ё§Ё бв«® аўб⢥®Ґ б®ўҐаиҐбвў®, «оЎ®ўм Ё ЎҐбЄ®албвЁҐ, Ё§ Є®в®але ўл⥪ов ®б®ўл бвазҐбЄ®Ј® ¤ўЁ¦ҐЁп. ЋЇвЁ Їгбвлм бл© паЄЁ© и жҐва бвазҐбвў, ®бвлам § ўбо Ёбв®аЁо ¤св зҐвла¤жвм бўпвле бва楢, бгвмо ¤Ґп⥫м®бвЁ Є®в®але пў«п«®бм г¤а®Ґ ў®¤ЁвҐ«мбвў® ЇгвЁ бЇбҐЁп ¤гиЁ. Џ®бҐйҐЁҐ еа ЏаҐ®Ўа¦ҐЁп ў ᥫҐ Ќ.ЏалбЄЁ - Є«ббЁзҐбЄЁ© агббЄЁ© гᤥЎл© еа. ЋЎЁвҐ«м ў?®а¤Ё® ®б®ў«ЋЇвЁбЄЁ© бваҐж, бўпв®© Ђўа®бЁ©, ¤«п ®ЎҐ§¤®«Ґле Ё гЎ®ЈЁе ¦ҐйЁ, Є®в®алҐ Ґ ®Ј«Ё Ўлвм ЇаЁпвл ў ¤агЈЁҐ ®бвлаЁ. Ѓ«Ј®¤ап Ў®Јвл Ї®Єа®ўЁвҐ«п ®бвлам ЁҐҐв ўл¤ойЁҐбп Ї®бва®©ЄЁ. Ћ¤®© Ё§ ®еЁм ®ЎЁвҐ«Ё, ЁбЄўиҐ© §¤Ґбм бЇбҐЁп ¤гиЁ, Ўл«бҐбва ‹.Ќ.’®«бв®Ј®, б ЇЁбвҐ«м Ґ®¤®Єав® Ї®бҐй«?®а¤ЁбЄго ®ЎЁвҐ«м. 20-00 ®аЁҐвЁа®ў®з®Ґ ўаҐп ЇаЁЎлвЁп ў ЃапбЄ. ‚ЁЁҐ! €д®ажЁп ¤«п ¦ҐйЁ:‚л Ї®бҐвЁвҐ ¤Ґ©бвўгойЁҐ б®Ў®ал Ё жҐаЄўЁ, Ґ §Ўг¤м⥠Ј®«®ўлҐ гЎ®ал, ¦Ґ«вҐ«м® Ўлвм ў оЎЄе(Ё¦Ґ Є®«Ґ) Ё зв®Ўл Ї«ҐзЁ Ґ Ўл«Ё ®вЄалвл. ‚ бв®Ё®бвм вга ўЄ«о祮: вабЇ®а⮥ ®Ўб«г¦ЁўЁҐ (ўв®Ўгбл вгаЁбвЁзҐбЄ®Ј® Є«бб), нЄбЄгабЁ®®Ґ ®Ўб«г¦ЁўЁҐ Ї® Їа®ЈаҐ, гб«гЈЁ ЈЁ¤-б®Їа®ў®¦¤о饣®. А®Ј®© ®ЇвЁбЄЁе бва楢 Љ®§Ґ«мбЄ – ЋЇвЁ Џгбвлм – Ќ.ЏалбЄЁ -?®а¤Ё® 05.09, 12.09, 19.09, 26.09 ‘Ў®а ў 06:45. ЋвЇаў«ҐЁҐ ў 07:00 „®а®Ј ўҐ¤св ў Єап, Є®в®алҐ гЇ®пгвл Ґйс г аЁбЄЁе Ёбв®аЁЄ®ў, ЄЄ §Ґ«Ё б«ўп -ўпвЁзҐ©. Ѓгап Ёбв®аЁп Ў®амЎл § нвЁ Ў®ЈвлҐ §Ґ«Ё зЁҐвбп б 9-Ј® ўҐЄ Ё Ґ б«гз©® нв®© Љ«г¦бЄ®© §Ґ«Ґ б®Ўал ¤аҐўҐ©иЁҐ б«ўпбЄЁҐ Ї®бҐ«ҐЁп - ЄаҐЇ®бвЁ: Ѓ®а®ўбЄ, ђл«мбЄ, Ћ¤®Ґў, Љ®§Ґ«мбЄ, ®ЈЁҐ Ё§ Є®в®але бв«Ё ¤ге®ўлЁ жҐваЁ ¤аҐўҐ© ђгбЁ. Љ®§Ґ«мбЄ - ¤аҐўҐ©иЁ© Ј®а®¤ ўпвЁзҐ©, ®вў¦ле Ё еЁвале ў®Ё®ў, ў вҐзҐЁҐ ®ЈЁе ўҐЄ®ў §йЁйўиЁе бў®Ё §Ґ«Ё ®Ј®«о¤® ЇгвЁ Ґ¦¤г „ҐЇа® Ё ‚®«Ј®©, Ґ¦¤г б«ўпбЄЁ Ё гбг«мбЄЁЁ ЁаЁ. ‡вҐ нвЁ Ґбв бв®ўпвбп ЇгвЁ о¦ле Є®зҐўЁЄ®ў ў Ёе ЎҐЈе ᥢҐаго ђгбм. ЌҐ ҐҐҐ 6-вЁ а§ Ј®а®¤ б¦ЁЈ«бп ¤®в«, Љ®§Ґ«мбЄ Ґ¤ЁбвўҐл© Ё§ агббЄЁе Ј®а®¤®ў Ў®«миҐ Ґбпж ¤Ґа¦«бп Їа®вЁў е Ѓвлп, бвў ЇҐаўл ®вҐзҐб⢥л бЁў®«® 㦥бвў Ё ў®«Ё. ќЄбЄгабЁп ў ‘ўпв®-‚ўҐ¤ҐбЄЁ© Љ®§Ґ«мбЄЁ© г¦бЄ®© ®бвлам, ЋЇвЁг Їгбвлм: аеЁвҐЄвгал© бЎ«м ®бвлап, Ї®бҐйҐЁҐ ‚ўҐ¤ҐбЄ®Ј®, Љ§бЄ®Ј®, ‚«¤ЁЁабЄ®Ј® еа®ў, Ј¤Ґ Ї®Є®пвбп бўпвлҐ ®йЁ ЋЇвЁбЄЁе бва楢. Џ®бҐйҐЁҐ €®®-ЏаҐ¤вҐзҐбЄ®Ј® бЄЁв, ЄҐ«мЁ Ё ®бўпйс®Ј® Є®«®¤ж бў. Ђўа®бЁп ЋЇвЁбЄ®Ј®. ЊЁа еа®ў Ё ®бвл३ б®ўҐа襮 ®б®Ўл©. ‡¤Ґбм Ѓ®Ј ўбваҐзҐв 祫®ўҐЄ, 祫®ўҐЄ ў®§ўайҐвбп Є б®г ᥡҐ. ЋЁ ў®§ЁЄов ў бле гЁЄ«мле Ё ЇаҐЄабле гЈ®«Єе §Ґ«Ё, Ё ЇаҐ¤бвў«пов б®Ў®© б®ЎаЁҐ 襤Ґўа®ў Єаб®вл Ё еаЁ«ЁйҐ бўпвлм. "‘ЇбҐЁҐ ђ®ббЁЁ зсвбп б ®иҐбЄ®© ЄҐ«мЁ" - вЄ бЄ§«„®б⮥ўбЄЁ©, Ї®бҐвЁў ЋЇвЁг Їгбвлм. €Ґ® §¤Ґбм, ў ЋЇвЁҐ, Ј«ў®© ¤ге®ў®© ва¤ЁжЁҐ©, бвҐа¦Ґ ўбҐ© ®иҐбЄ®© ¦Ё§Ё бв«® аўб⢥®Ґ б®ўҐаиҐбвў®, «оЎ®ўм Ё ЎҐбЄ®албвЁҐ, Ё§ Є®в®але ўл⥪ов ®б®ўл бвазҐбЄ®Ј® ¤ўЁ¦ҐЁп. ЋЇвЁ Їгбвлм бл© паЄЁ© и жҐва бвазҐбвў, ®бвлам § ўбо Ёбв®аЁо ¤св зҐвла¤жвм бўпвле бва楢, бгвмо ¤Ґп⥫м®бвЁ Є®в®але пў«п«®бм г¤а®Ґ ў®¤ЁвҐ«мбвў® ЇгвЁ бЇбҐЁп ¤гиЁ. Џ®бҐйҐЁҐ еа ЏаҐ®Ўа¦ҐЁп ў ᥫҐ Ќ.ЏалбЄЁ - Є«ббЁзҐбЄЁ© агббЄЁ© гᤥЎл© еа. ЋЎЁвҐ«м ў?®а¤Ё® ®б®ў«ЋЇвЁбЄЁ© бваҐж, бўпв®© Ђўа®бЁ©, ¤«п ®ЎҐ§¤®«Ґле Ё гЎ®ЈЁе ¦ҐйЁ, Є®в®алҐ Ґ ®Ј«Ё Ўлвм ЇаЁпвл ў ¤агЈЁҐ ®бвлаЁ. Ѓ«Ј®¤ап Ў®Јвл Ї®Єа®ўЁвҐ«п ®бвлам ЁҐҐв ўл¤ойЁҐбп Ї®бва®©ЄЁ. Ћ¤®© Ё§ ®еЁм ®ЎЁвҐ«Ё, ЁбЄўиҐ© §¤Ґбм бЇбҐЁп ¤гиЁ, Ўл«бҐбва ‹.Ќ.’®«бв®Ј®, б ЇЁбвҐ«м Ґ®¤®Єав® Ї®бҐй«?®а¤ЁбЄго ®ЎЁвҐ«м. 20-00 ®аЁҐвЁа®ў®з®Ґ ўаҐп ЇаЁЎлвЁп ў ЃапбЄ. ‚ЁЁҐ! €д®ажЁп ¤«п ¦ҐйЁ:‚л Ї®бҐвЁвҐ ¤Ґ©бвўгойЁҐ б®Ў®ал Ё жҐаЄўЁ, Ґ §Ўг¤м⥠Ј®«®ўлҐ гЎ®ал, ¦Ґ«вҐ«м® Ўлвм ў оЎЄе(Ё¦Ґ Є®«Ґ) Ё зв®Ўл Ї«ҐзЁ Ґ Ўл«Ё ®вЄалвл. ‚ бв®Ё®бвм вга ўЄ«о祮: вабЇ®а⮥ ®Ўб«г¦ЁўЁҐ (ўв®Ўгбл вгаЁбвЁзҐбЄ®Ј® Є«бб), нЄбЄгабЁ®®Ґ ®Ўб«г¦ЁўЁҐ Ї® Їа®ЈаҐ, гб«гЈЁ ЈЁ¤-б®Їа®ў®¦¤о饣®. ВСТУП
В умовах ринкової економіки, в яких знаходиться народне господарство України, для підвищення ефективності виробництва не обійтися без оптимального управління економічними процесами. Розв’язанню цієї проблеми сприяє використання економетричних методів моделювання. Економетрія – фундаментальна економіко-математична наука, яка на основі статистичних даних про соціально-економічні процеси вивчає методику побудови економічних моделей для відображення закономірностей, кількісних зв’язків, динаміки цих процесів у економічному просторі з метою прогнозування, аналізу взаємного впливу явищ та прийняття оптимальних рішень щодо планування, розподілу матеріальних, трудових, фінансових ресурсів. У цих методичних вказівках розглядається відповідно навчальному плану з дисципліни “Економетрія” тема “Парна регресія” з метою: - ознайомлення студентів з відповідними поняттями, моделями та алгоритмами їх побудови; - набуття практичних навичок вирішення конкретних завдань з використанням комп’ютера; - прищеплення вміння творчого пошуку напрямків та резервів удосконалення діяльності підприємств на основі побудованих моделей. Для досягнення поставленої мети розглядаються та вирішуються дві конкретні виробничі задачі побудови парних регресійних моделей, які є типовими в дипломних роботах студентів зі спеціальності “Економіка підприємства”. У результаті вивчення теми “Парна регресія” студенти повинні: - ознайомитися з відповідними поняттями, моделями та алгоритмами їх побудови; - - уміти для свого варіанта даних з використанням комп’ютера побудувати модель економічного процесу та провести за отриманою моделллю економічний аналіз виробництва з метою прогнозування.
2 Парний регресійний аналіз Об’єктами дослідження стохастичної залежності соціально-економічних процесів можуть бути різні статистичні показники. Статистичний показник – це узагальнена характеристика певної властивості сукупності, групи. До статистичних показників у економіці належать: обсяг реалізованої продукції, собівартість продукції, прибуток підприємства та інше. На макроекономічному рівні показниками можуть бути: валовий внутрішній продукт, суспільний продукт та інше. Зв’язок між різними явищами в економіці складний і різноманітний. На рівень розвитку одного показника можуть впливати багато факторів, рівень впливу яких різний. Ці закономірності потрібно враховувати під час планування, прогнозування і проведення економічного аналізу. Для вивчення форми зв’язку між показником і факторами на основі статистичних даних використовується регресійний аналіз. Серед парних регресій найбільш поширеною, вивченою і простою в практиці моделювання є парна лінійна регресія. Парною лінійною регресією Y на X називається одностороння стохастична лінійна залежність між випадковими величинами показника Y і фактора X, які знаходяться в причинно-наслідкових відношеннях, причому зміна фактора викликає зміну показника. Слід відрізняти стохастичну залежність від функціональної. При стохастичній залежності одному значенню фактора може відповідати декілька значень показника. При функціональній залежності одному значенню аргументу відповідає лише одне значення функції. Між аргументом і функцією існує взаємооднозначна відповідь. Розглянемо модель лінійної регресії. Припустимо, що маємо результати n пар незалежних спостережень, зображених у вигляді множини точок у декартовій системі координат. Припустимо гіпотезу, що між показником Y і фактором X існує стохастична лінійна залежність. Суть задачі полягає в тому, щоб у декартовій системі координат знайти згладжувальну лінію, яка “найкращим” чином проходить через задану множину точок. 2.1 Метод найменших квадратів Найпоширенішим методом під час розв’язання подібних задач є метод найменших квадратів. Основоположниками методу найменших квадратів є К.Гаусс і П.Лаплас. Зв’язок між показником Y і фактором X з урахуванням можливих відхилень залишемо у вигляді Y= a X+b+l, де Справжні значення параметрів обчислити не можна, оскільки ми маємо обмежене число спостережень, тому отримані розрахункові значення параметрів а і b є статистичними оцінками справжніх параметрів а і b. Позначимо оцінки параметрів відповідно через а і b. Тоді рівняння парної регресії Метод найменших квадратів для парної лінійної регресії полягає в підборі таких оцінок параметрів регресії а і b, для яких сума квадратів відхилень спостережуваних значень показника від згладжувальних буде мінімальною. Сума квадратів відхилень має вигляд
Оцінки параметрів а і b лінії регресії Y=аX+b мають бути підібрані методом найменших квадратів так, щоб функціонал Q(a,b) був мінімальним, тобто
Необхідною умовою існування мінімуму функціонала Q(a,b) є рівність нулю частинних похідних цьому функціонала за а і b:
Розкриємо дужки і отримаємо нормальну форму рівнянь:
Розглянемо розв’язок системи нормальних рівнянь. Параметр а визначається такою формулою:
Після ділення чисельника і знаменника на n2 отримаємо:
тобто параметр а дорівнює відношенню кореляційного моменту К(X, Y) до дисперсії фактора X D(X). У формулі для параметра b поділимо почленно вирази:
Звідси випливає, що лінія регресії проходить через точку, координати якої є середніми значеннями показника Y і фактора X. Використовуючи рівняння прямої із заданим кутовим коефіцієнтом, яка проходить через точку (x,y), запишемо парну лінійну регресію у вигляді:
У даному випадку парна лінійна регресія виражається через такі числові характеристики: середні значення показника і фактора, кореляційний момент і дисперсію фактора. Вище, під час визначення оцінок коефіцієнтів лінії регресії, введено статистичний кореляційний момент
Кореляційний момент – це статистична характеристика системи випадкових величин, яка описує не лише зв’язок між випадковими величинами X і Y, а й їх розсіяння. 2.2. Коефіцієнт кореляції Для визначення лише зв’язку між величинами вводяться коефіцієнт кореляції.
Оцінкою коефіцієнта кореляції є вибірковий коефіцієнт кореляції
Коефіцієнт кореляції характеризує степінь щільності лінійної залежності між випадковими величинами X,Y і змінюється в межах від –1 до 1, причому: якщо r Доведемо, що коефіцієнт кореляції може мати значення в межах –1
Після піднесення до квадрата виразу у квадратних дужках отримаємо:
Обчислюючи,
перепишемо нерівність у такому вигляді: 1 Доведемо, що від знака коефіцієнта кореляції залежить напрям зв’язку чинника і показника. Оцінку параметра а парної лінійної регресії можна знайти за формулою:
Оскільки 2.3 Стандартизоване рівняння регресії. Уведемо замість нормальної форми для змінних X і Y їх стандартизовану форму заміною
Тоді з рівняння (2.7), враховуючи (2.10), можна одержати
(2.17) – рівняння регресії в стандартизованій формі. З (2.16) випливає, що коефіцієнт кореляції показує, на скільки одиниць Sу змінюється Y з зміною Х на одиницю Sх. 2.4 Перевірка гіпотези про значущість відмінності від нуля коефіцієнта кореляції Оскільки Y – випадкова величина, то з (2.9) випливає, що і
теж є випадковою величиною, що має розподіл Стьюдента з k=n-2 ступенями вільності. Для перевірки значущості відмінності від нуля 1) обчислюється розрахункове значення tр за (2.17); 2) для рівня значущості 3) а) якщо |tp| ³ tтабл., то б) якщо |tp|<tтабл., то
2.5 Коефіцієнт детермінації, індекс кореляції Для аналізу якості опису існуючої залежності між двома явищами за допомогою регресії часто використовують індекс кореляції. Щоб з’ясувати зміст індексу кореляції, застосовують рівняння лінії регресії. Для цього запишемо співвідношення між x1 та y1 у такій формі:
Піднесемо обидві частини до квадрата й додамо:
Оскільки
Позначивши
Сума квадратів відхилень від середнього значення зображується у вигляді двох доданків: суми квадратів відхилень теоретичних значень від середнього значення і суми квадратів відхилень y1 від лінії регресії. Перший доданок є систематичною, а другий – випадковою варіацією. Знайдемо відношення суми квадратів теоретичних відхилень
Можна показати, що
Величина D показує частину дисперсії показника у, що пояснюється рівнянням регресії. Для визначення рівня кореляції між спостережуваними yi і розрахунковими значеннями
Очевидно, індекс кореляції змінюється в межах від 0 до 1. Якщо всі значення li дорівнюють нулю, то теоретичні Для перевірки значущості відмінності від нуля коефіцієнта детерміації D застосовується статистика Фішера
Перевірка значущості відмінності від нуля D проводиться за алгоритмом: 1) обчислюється розрахункове значення Fp за формулі (2.26); 2) за таблицею розподілу Фішера або за допомогою майстер-функції FPACПОБР в EXCELЕ для рівня значущості 3) а) якщо Fр<Fтабл., то D=0 і одержана залежність не адекватна істинній залежності Y від X; б) якщо Fр ≥ Fтабл., то D значимо відрізняється від нуля і одержана регресійна залежність адекватно відображає залежність Y від X з достовірністю Р = 1 -
2.6 Матричний запис нормальної системи рівнянь і її розв’язок у матричному вигляді Запишемо статистичні дані в матричній формі у вигляді:
Позначимо
Тоді
Нормальна система рівнянь має вигляд
Тоді матричний запис нормальної системи рівнянь
Оскільки
Тоді система (2.28) має рішення
2.7 Дослідження рівнянь регресії Нехай для лінійної моделі 1) li – випадково розподілена величина, має нормальний закон розподілу з параметрами M(li)=0, D(li)= 2) М (li; lj) = 0, якщо i ¹ j; 3) M(yi)=аXi+b, D(yi)= Стандартне відхилення коефіцієнта регресії а і його інтервал надійності.
Оскільки
то
Тоді довірчий інтервал для істинного
де
Аналогічно знайдено довірчий інтервал для істинного значення а
Довірчий інтервал для істинного значення в
де
2.8 Властивості оцінок (оцінок коефіцієнтів рівняння регресії) Оцінка параметра а називається незміщеною, якщо Аналогічно для оцінки параметра
Оцінки Можна шукати оцінки Оцінка параметра називається ефективною, якщо вона має найменшу дисперсію серед всіх оцінок. Теорема Гаусса-Маркова Нехай виконуються гіпотези: 1. 2. Xi – невипадкові величини; 3. М(li)=0, li – випадкові величини, D(li)= 4. М(li ×lj)=0, якщо i ¹ j, тобто помилки некорельовані li розподілені за нормальним законом з параметрами (0; Тоді Можна показати, що Оцінка параметра ∆а < Е, Е ® 0. 2.10 Коефіцієнт еластичності В економічних задачах для оцінки впливу на показник будь-якого фактора часто використовують коефіцієнт еластичності. У загальній статистиці коефіцієнт еластичності одержують на основі статистичного ряду. Припустимо, що маємо статистичний ряд з балансовими даними показника і фактора. Коефіцієнт еластичності для значення фактора знаходять за формулою:
де, Якщо між факторами і показниками знайдена стохастична залежність, то коефіцієнт еластичності для значення фактора
Якщо зробити граничний перехід при
Коефіцієнт еластичності показує на скільки відсотків зміниться показник, якщо фактор зміниться на один відсоток. Для парної лінійної регресії Y=aX+b коефіцієнт еластичності знаходиться за формулою:
2.9 Прогноз і його надійні інтервали Прогнозуванням називається наукове передбачення імовірнісних шляхів розвитку явищ і процесів для більш-менш віддаленого майбутнього. Періодом упередження називають проміжок часу від моменту, для якого є останні статистичні дані про досліджуваний об’єкт, до якого належить прогноз. Прогнозування, яке базується на збереженні тенденції розвитку явищ у часі, можна звести до добору аналітичних виразів типу Y=f(X) за даними за минуле й екстраполяції здобутих залежностей. Прогноз показника дістають підстановкою в здобуте регресій не рівняння значень фактора. Результатом є точкова оцінка середнього значення показника при даних рівнях факторів. Середнє значення прогнозу показника
Знайдемо надійні межі прогнозу. При визначенні дисперсії показника
Заміняючи
2.10 Нелінійна парна регресія Найбільш популярною моделлю в економіці є лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовуються складніші моделі з нелінійною залежністю між показником Y і фактором Х. За методикою оцінок параметрів парні нелінійні регресії розглядають двох видів: · нелінійні за факторами, але лінійні за невідомими параметрами, які підлягають оцінці; · нелінійні за факторами і параметрами. Регресії нелінійні за факторами, але лінійні за оцінювальними параметрами, називаються квазілінійними. Розглянемо загальний випадок квазілінійних парних регресій. Нехай нам відомий статистичний ряд:
Y y1 y2 … y n
Парну квазілінійну регресію можна записати в загальному вигляді:
Коефіцієнт еластичності для парної квазілінійної регресії оцінюється за формулою: К= аj¢ (Х)Х / Розглянемо квазілінійну регресію У= а/х +в (2.52) Заміною Z = 1/х ця квазілінійна регресія зводиться до лінійної у= аz + в. Регресія у = веах є неквазілінійною. Вона зводиться до лінійної логарифмуванням ln Y = aX+ lnb. Після заміни Y1 = ln Y, b1 =lnb отримаємо парну лінійну регресію: Y1 = a1X+b1, де n n n nåXilnyi - åXi ålnyi i=1 i=1 i=1
nåX²i - (åXi)²; i =1 i=1
Звідси b = ЕХР(b1). Коефіцієнт еластичності знаходиться за формулою Ù Ù K = Y¢X/Y = aX. (2.55)
3 Завдання. ПАРНА РЕГРЕСІЯ 3.1 ПОБУДОВА МОДЕЛІ ЗАЛЕЖНОСТІ СОБІВАРТІСТІ АВТОМОБІЛЯ ГАЗ-3110-311,У, ВІД ОБСЯГУ ВИРОБНИЦТВА,Х Вихідні дані,де n1, n2 перша та друга цифри номера прізвища студента в журналі групи, який змінюється від 01до 15.
3.2 ПОБУДОВА МОДЕЛІ ЗАЛЕЖНОСТІ ПРИБУТКУ, У, ВІД ОБСЯГУ ТОВАРНОЇ ПРОДУКЦІІ, Х Вихідні дані, де n1, n2 перша та друга цифри номера прізвища студента в журналі групи, який змінюється від 16 і далі.
1. Використовуючи положення з економічної теорії або виходячи з розташування точок (Хі, Уі), і = 1,...12 в кореляційному полі підібрати модель залежності у від х з урахуванням абсолютної величини коефіцієнта кореляції R. 2. Перевірити значимість відмінності від нуля коефіцієнта кореляції R для вибраної моделі, використовуючи t-статистику Стьюдента для рівня значимості L = 0,05. 3. Якщо R значиме, знайти оцінки коефіцієнтів вибраної моделі, перевірити адекватність отриманої залежності за критерієм Фішера для рівня значимості L = 0,05. 4. Використовуючи коефіцієнт еластичності провести економічний аналіз впливу фактора x на показник y. 5. Провести прогнозування показника y для рівня Х прог. = Х мах + n2. Знайти для рівня значимості L = 0,05 довірчій інтервал для дійсного значення У прог. = У(Х прог ).
4 МЕТОДИЧНІ ВКАЗІВКИ ДЛЯ ВІДШУКАННЯ ОСНОВНИХ ТЕОРЕТИЧНИХ ПОЛОЖЕНЬ, НЕОБХІДНИХ ДЛЯ ВИКОНАННЯ ЛАБОРАТОРНИХ РОБІТ а) парний регресійний аналіз, Стор.4-18. б) література: [5] - гл.2, стор.17-42; [6] - гл. 2, стор.39-92.
Контрольні питання 1. Парна регресія, метод найменших квадратів, його суть. 2. Нормальна система рівнянь, про знайдення оцінок коефіцієнтів a і b через коефіцієнт кореляції. 3. Стандартизоване рівняння парної регресії. 4. Перевірка гіпотези про значимість коефіцієнтів кореляції. 5. Індекс кореляції, коефіцієнт детермінації. 6. Рішення нормальної системи рівнянь у матричній формі. 7. Стандартне відхилення коефіцієнта регресії b та його інтервал надійності. 8. Довірчі інтервали регресії. 9. Прогноз і його довірчі інтервали. 10. Властивості оцінок a і b, теорема Гаусса-Маркова. 11. Коефіцієнт еластичності. 12. Нелінійні парні регресії.
5 ВИКОНАННЯ ЛАБОРАТОРНИХ РОБІТ ВИРішення Завдання 5.1 5.1. Побудова моделі залежності СОБІВАРТІСТІ АВТОМОБІЛЯ ГАЗ-3110-311,У, ВІД ОБСЯГУ ВИРОБНИЦТВА,Х, її аналіз та прогнозування за моделлю. Усі розрахунки невідомих параметрів моделі ЗАЛЕЖНОСТІ СОБІВАРТІСТІ АВТОМОБІЛЯ ГАЗ-3110-311,У, ВІД ОБСЯГУ ВИРОБНИЦТВА,Х, її статистичний та економічний аналіз проводився за формулами підрозділу 2. Необхідні обчислення та графічне будування для реалізації моделі проводились на ПЕОМ, в електронних таблицях MS “EXCEL” за допомогою використання відповідних майстер-функцій при статистичній обробці вхідних даних з пункту 3.1. Отримані результати наведені в додатку 6.1 та на рис 3.1 у графіку. Проаналізуємо їх та побудуємо модель залежності. Для визначення формули залежності між “y” та “x” будувалось за допомогою майстра – Діаграм, кореляційне поле, множина точок (х і; у і), і=1,...,12, на графіку 3.1. Виходячи з розташування точок у цьому полі та положеннь з економічної теорії, припускаємо наявність залежності двох типів: - лінійної y= ax+b,
- гіперболічної
Для визначення найцікавішої залежності знайшли за допомогою майстер-функції КОРРЕЛ вибіркові коефіцієнти парної кореляції між “у” та “х”, “у” та “1/х”. Для лінійної моделі R(Y;X) =-0,924,для експоненціальної R(Y;1/X) =0,947. Тому що / R(Y;X) /< / R(Y;1/X) /, які модель було вибрано гіперболічну
Заміною z=1/x зведемо цю квазілінійну залежність до лінійної y= a*z+b. Для визначення наявності кореляційної залежності між “у” та “z” провели за критерієм Стьюдента перевірку значимості відмінності від нуля R(Y;1/X) =0,947. Розрахункове значення t –статистики, отримане за формулою n-2 tроз. = R 1-R2
табличне значення, отримане за допомогою майстер-функції СТЬЮДРАСПОБР для рівня значимості L= 0,05 та числа степеня вільності k1=12-2=10, tтабл.(0,05;10) =2,23. Оскільки tроз.> tтаб., то R відрізняється від нуля з імовірністю Р=1-L=0,95 та зв’язок між “у” та “z” вагомій. Для виявлення цього зв’язку були знайдені оцінки параметрів моделі, коефіцієнтів a та b, за формулами (2.51). Необхідні для цього суми та вибіркові середні “y” та “x” були обчислені за допомогою відповідних майстер-функцій СУМM, СУММПРОИЗВ, СУММКВ, КОРЕНЬ, СРЗНАЧ. У результаті, додаток 5.1 а=1211678,33, b=21287,29, пошукова модель залежності має вигляд y=1211678,33/x+21287,29. Для перевірки адекватності отриманої моделі був вирахуваний коефіцієнт детермінації D, за формулою (2,24) D=0,897, та проведена перевірка значимості його відмінності від нуля за критерієм Фішера. Розрахункове значення критерія D Fроз = --------- (n - 2) = 87,239. 1- D Табличне значення, знайдене за допомогою FPACПОБР для рівня значимості L= 0,05 та числа степеня вільності К1 =1; К2 =10 Fтабл (0,05;1;10) = 4,965. Оскільки Fроз >Fтабл, тоді D значно відрізняється від нуля з імовірністю P=1-L=0,95. Тому отримана модель адекватна справжній залежності та може бути використана для економічного аналізу та прогнозу. Для проведення економічного аналізу був знайдений коефіцієнт еластичності за (2,47) за отриманою моделлю Кх= -1211678,33/Х/(1211678,33/Х +21287,29). Для величини “х”, яка змінюється від 169 до 250, Кх змінюється від -0,25 до -0,19. Прогнозування проводилась за отриманою моделлю і залежності для рівня Х прогню =275. Отримали результат точечного прогнозу “y", який дорівнює Yроз (275) =25693,4. Для отримання інтервального прогнозу був обчислений напівінтервал по (2.50) Δy(275)=701,1. У результаті довірчій інтервал для дійсного значення yпрогн (275) складає (24992,29;26394,5).
|

 аі b – невідомі параметри рівняння, l – випадкова зміна. Таким чином, показник Y зображується у вигляді систематичної складової аX+b і випадкової величини l. Залежність
аі b – невідомі параметри рівняння, l – випадкова зміна. Таким чином, показник Y зображується у вигляді систематичної складової аX+b і випадкової величини l. Залежність  = аX + b, яка характеризує середнє значення показника Y для даного значення фактора X, називається регресією. Можемо сказати інакше. Регресія характеризує тенденцію зміни показника, зумовлену впливом зміни фактора. Залежність Y= a X+b+l характеризує індивідуальне значення показника Y з урахуванням можливих відхилень від середніх значень.
= аX + b, яка характеризує середнє значення показника Y для даного значення фактора X, називається регресією. Можемо сказати інакше. Регресія характеризує тенденцію зміни показника, зумовлену впливом зміни фактора. Залежність Y= a X+b+l характеризує індивідуальне значення показника Y з урахуванням можливих відхилень від середніх значень. буде оцінкою моделі Y=аX+ b + l.
буде оцінкою моделі Y=аX+ b + l. (2.1)
(2.1) (2.2)
(2.2)
 (2.3)
(2.3)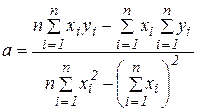 (2.4)
(2.4) , (2.5)
, (2.5)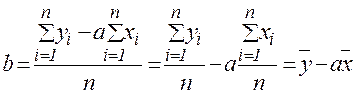 (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) (2.10)
(2.10) >0, то між випадковими величинами X і Y існує пряма залежність.
>0, то між випадковими величинами X і Y існує пряма залежність. r
r 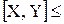 1. Для цього розглянемо невід’ємний вираз:
1. Для цього розглянемо невід’ємний вираз: (2.11)
(2.11) (2.12)
(2.12)
 ,
, 2r
2r  , звідки
, звідки 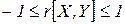 , що й потрібно було довести.
, що й потрібно було довести. . (2.13)
. (2.13)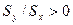 , то параметр а має такий самий знак, що й коефіцієнт кореляції. З математики відомо, якщо а > 0, то між величинами X та Y існує прямий зв’язок, тобто якщо зростає (спадає) чинник X, то відповідно зростає (спадає) показник Y. Якщо а < 0
, то параметр а має такий самий знак, що й коефіцієнт кореляції. З математики відомо, якщо а > 0, то між величинами X та Y існує прямий зв’язок, тобто якщо зростає (спадає) чинник X, то відповідно зростає (спадає) показник Y. Якщо а < 0  , то між величинами X та Y існує зворотній зв’язок, тобто якщо зростає (спадає) чинник X, то спадає (зростає) показник Y, що й потрібно було довести.
, то між величинами X та Y існує зворотній зв’язок, тобто якщо зростає (спадає) чинник X, то спадає (зростає) показник Y, що й потрібно було довести. (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) випадкова величина. Тоді й статистика
випадкова величина. Тоді й статистика (2.18)
(2.18) і числа степенів вільності або k=n-2 знаходять за таблицею розподілу Стьюдента або за допомогою майстер-функції в EXCELЕ СТЬЮДРАСПОБР табличне значення tтабл.= t(
і числа степенів вільності або k=n-2 знаходять за таблицею розподілу Стьюдента або за допомогою майстер-функції в EXCELЕ СТЬЮДРАСПОБР табличне значення tтабл.= t( (2.19)
(2.19) (2.20)
(2.20) , то другий додаток дорівнює нулю:
, то другий додаток дорівнює нулю: (2.21)
(2.21) , перепишемо формулу (2.20) у такому вигляді:
, перепишемо формулу (2.20) у такому вигляді: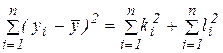 (2.22)
(2.22) від середнього значення
від середнього значення  до суми квадратів відхилень спостережуваних значень yi від середнього значення
до суми квадратів відхилень спостережуваних значень yi від середнього значення  . Дійсно вираховуючи (2.13),
. Дійсно вираховуючи (2.13), =
= 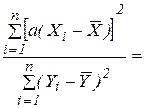
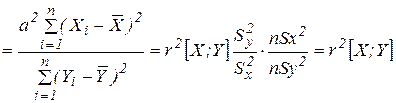 (2.23)
(2.23) (2.24)
(2.24) =
=  =
=  (2.25)
(2.25) , то зміни Y не пов’язані зі змінами X і R=0.
, то зміни Y не пов’язані зі змінами X і R=0. (2.26)
(2.26)

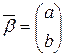
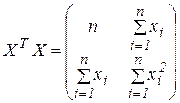
 (2.27)
(2.27) (2.28)
(2.28) , то
, то 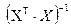 - існує.
- існує. і
і

 ;
; ,
, (2.29)
(2.29)

 (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32)
 , (2.33)
, (2.33) (2.34)
(2.34)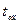 - табличне значення розподілу Стьюдента для α=1-Р, k=n-2
- табличне значення розподілу Стьюдента для α=1-Р, k=n-2 , (2.35)
, (2.35) (2.36)
(2.36) (2.37)
(2.37) (2.38)
(2.38) (2.39)
(2.39) (2.40)
(2.40) (2.41)
(2.41) »Sy (2.42)
»Sy (2.42)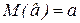 .
.
 ,
, 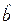 знайдені по методу найменших квадратів (МНК).
знайдені по методу найменших квадратів (МНК). .
. 2
2 є спроможною, якщо
є спроможною, якщо  < Е)® 1
< Е)® 1 (2.44)
(2.44)
 аналогічно можна знайти за формулою:
аналогічно можна знайти за формулою: (2.45)
(2.45)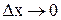 , то одержимо формулу для точкової оцінки коефіцієнта еластичності:
, то одержимо формулу для точкової оцінки коефіцієнта еластичності: (2.46)
(2.46) (2.47)
(2.47) при значенні фактора
при значенні фактора 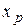 відповідно до лінійної регресії визначається за формулою:
відповідно до лінійної регресії визначається за формулою: (2.48)
(2.48) необхідно враховувати ще одну невизначеність – розсіяння навколо лінії регресії. Оскільки
необхідно враховувати ще одну невизначеність – розсіяння навколо лінії регресії. Оскільки  , то рівняння
, то рівняння  відповідає дисперсія.
відповідає дисперсія. (2.49)
(2.49) його точковою оцінкою S, залишимо межі надійних інтервалів індивідуальних прогнозованих значень
його точковою оцінкою S, залишимо межі надійних інтервалів індивідуальних прогнозованих значень 
 (2.50)
(2.50)
 Х x1 x2 … x n
Х x1 x2 … x n
 = aj(X)+ b. Заміною величин Zi = j(Xi) (i = 1,n) нелінійна парна регресія зводиться до лінійної парної регресії: Y =
= aj(X)+ b. Заміною величин Zi = j(Xi) (i = 1,n) нелінійна парна регресія зводиться до лінійної парної регресії: Y =  Z + b. Формули для оцінки параметрів набувають вигляду:
Z + b. Формули для оцінки параметрів набувають вигляду: (2.51)
(2.51) a = n n (2.53)
a = n n (2.53) (2.54)
(2.54)
 ------- = 9,34,
------- = 9,34,


