Уравнения линии конечной длины
Постоянные
определяются на основании граничных условий.
Тогда из (5) и (6) получаем
откуда
Подставив найденные выражения
Уравнения (7) и (8) позволяют определить ток и напряжение в любой точке линии по их известным значениям в начале линии. Обычно в практических задачах бывают заданы напряжение
Обозначив
откуда
После подстановки найденных выражений
Уравнения длинной линии как четырехполюсника В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.
|

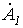 и
и  в полученных в предыдущей лекции формулах
в полученных в предыдущей лекции формулах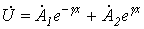 ;
;

 Пусть для линии длиной l (см. рис. 1) заданы напряжение
Пусть для линии длиной l (см. рис. 1) заданы напряжение  и ток
и ток  в начале линии, т.е. при
в начале линии, т.е. при  .
.
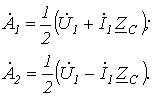


 и ток
и ток  в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде
в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде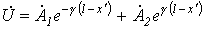 ;
;
 .
.
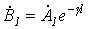 и
и  , из уравнений (9) и (10) при
, из уравнений (9) и (10) при  получим
получим
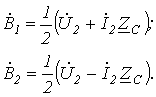
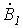 и
и  в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии
в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии ;
;
 .
.
 ;
; .
.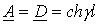 ;
;  и
и  ; при этом условие
; при этом условие  выполняется.
выполняется.


