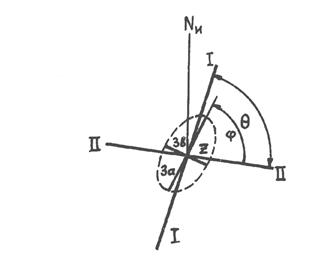
Пример. Секстаном измерили горизонтальный угол между ориентирами и
Секстаном измерили горизонтальный угол между ориентирами С карты сняли расстояния из счислимой точки до ориентиров, а также расстояние (базу) между ними: Вычислить модуль градиента горизонтального угла. Решение. По формуле:
получили: Градиент Оценка точности места судна методом эллипса погрешностей. Расчетные формулы элементов эллипса погрешностей. Влияние на обсервованное место судна случайных погрешностей измерений навигационных параметров наиболее полно и строго оценивается методом эллипса погрешностей. Эллипс погрешностей обладает следующими свойствами: - он является единственной фигурой, во всех точках которой плотность вероятности постоянна; - вероятность нахождения действительного места судна в пределах эллипса погрешностей больше, чем в любой другой фигуре, ограничивающей область такой же площади; - оси эллипса погрешностей показывают направление действия наибольшей и наименьшей погрешности обсервации. Расчет вероятности
При Если увеличить полуоси среднего эллипса в 1,1774 раз, то получим эллипс погрешностей, называемый вероятным. Для такого эллипса При Элементами эллипса погрешностей называют его большую
где
Угол Известно, что
Величину Формулы элементов эллипса погрешностей через смещения линий положения имеют вид:
Большая полуось эллипса погрешностей составляет меньший угол с более точной линией положения, т.е. с той линией положения у которой величина смещения меньше. Когда обе линии положения равноточны В открытом море производить оценку точности обсерваций для целей судовождения не требуется. Однако иногда такие задачи приходится решать при исследованиях радионавигационных и спутниковых систем, в частности, новых судовых приемоиндикаторов и новых методов измерений навигационных параметров. Таким образом, расчет элементов эллипса надо производить с такой точностью, которая соответствует точности обсервации и с учетом требований безопасности плавания. Пример. Место судна определено по двум визуальным пеленгам, Рассчитать элементы эллипса погрешностей и построить его главные оси по этим элементам, если Решение. 1. Составим формулы градиентов:
2. Вычисляем угол между линиями положения:
3. Составляем формулы для расчета элементов эллипса:
4. Подставляя числовые значения, произведем расчеты:
так как
5. По вычисленным элементам
Для этого в обсервованной точке
Рис. 1
|

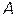 и
и 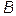 . Исправив поправками отсчет, взятый по шкале прибора, получили
. Исправив поправками отсчет, взятый по шкале прибора, получили  .
.



 или
или 
 направлен к центру окружности, проходящей через оба ориентира и вершину угла
направлен к центру окружности, проходящей через оба ориентира и вершину угла  (место судна).
(место судна). нахождения места судна в области, ограниченной эллипсом, производится по формуле:
нахождения места судна в области, ограниченной эллипсом, производится по формуле: (2).
(2).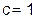 эллипс называют средним квадратическим или средним, или стандартным. Вероятность нахождения места судна
эллипс называют средним квадратическим или средним, или стандартным. Вероятность нахождения места судна  в границах среднего эллипса по формуле (2) составляет
в границах среднего эллипса по формуле (2) составляет 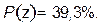
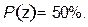
 получим
получим  При
При 
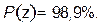 Эллипс погрешностей, которому соответствует такая вероятность, называют предельным. Его полуоси в три раза больше полуосей среднего эллипса.
Эллипс погрешностей, которому соответствует такая вероятность, называют предельным. Его полуоси в три раза больше полуосей среднего эллипса.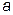 , малую
, малую  полуоси и угол
полуоси и угол 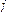 , служащий для ориентировки эллипса относительно линий положения. При определении места судна по двум линиям положения элементы среднего эллипса погрешностей вычисляют по формулам:
, служащий для ориентировки эллипса относительно линий положения. При определении места судна по двум линиям положения элементы среднего эллипса погрешностей вычисляют по формулам: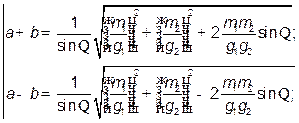 (3)
(3)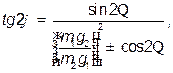 (4)
(4) - средние квадратические погрешности измерений навигационных параметров;
- средние квадратические погрешности измерений навигационных параметров; - модули градиентов навигационных параметров;
- модули градиентов навигационных параметров; - острый угол между первой и второй линиями положения.
- острый угол между первой и второй линиями положения. . Угол
. Угол  .
.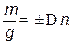 (5)
(5) называют смещением линии положения.
называют смещением линии положения. (6)
(6) (7)
(7) , то большая полуось эллипса направлена по биссектрисе острого угла
, то большая полуось эллипса направлена по биссектрисе острого угла  , зависит от вида обсерваций и применяемых ТСС, от условий плавания и, конечно, от того, какая информация о местоположении судна требуется для обеспечения безопасности плавания. Например, на подходе к берегу элементы эллипса целесообразно рассчитывать в милях с указанием десятых долей. В стесненных водах, где условия плавания значительно сложнее и, как правило, обеспечена более высокая точность обсерваций, полуоси эллипса следует вычислять до десятых долей кабельтова. Наконец, в узкостях, в зоне действия РНС ближнего действия и при хороших по точности обсервациях по НИСЗ может возникнуть надобность рассчитать элементы эллипса с точностью до десятых метров и даже до метров.
, зависит от вида обсерваций и применяемых ТСС, от условий плавания и, конечно, от того, какая информация о местоположении судна требуется для обеспечения безопасности плавания. Например, на подходе к берегу элементы эллипса целесообразно рассчитывать в милях с указанием десятых долей. В стесненных водах, где условия плавания значительно сложнее и, как правило, обеспечена более высокая точность обсерваций, полуоси эллипса следует вычислять до десятых долей кабельтова. Наконец, в узкостях, в зоне действия РНС ближнего действия и при хороших по точности обсервациях по НИСЗ может возникнуть надобность рассчитать элементы эллипса с точностью до десятых метров и даже до метров.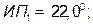 с карты сняли
с карты сняли 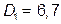 мили;
мили;  с карты сняли
с карты сняли 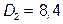 мили;
мили; 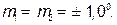



 =
=
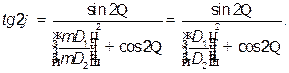


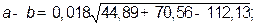

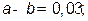



 имеет знак минус, угол
имеет знак минус, угол 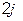 находится во второй четверти:
находится во второй четверти: и
и 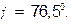

 и
и  построили на карте предельный эллипс ошибок:
построили на карте предельный эллипс ошибок: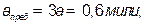
 .
. . Затем от точки
. Затем от точки  , как показано на рисунке (1)
, как показано на рисунке (1)