Рівняння (закону) динаміки обертального руху твердого тіла відносно нерухомої осі: похідна моменту імпульсу твердого тіла відносно осі дорівнює моменту сил відносно тієї ж осі.
Момент імпульсу замкнутої системи зберігається, тобто не змінюється з плином часу КІНЕТИЧНА ЕНЕРГІЯ ТІЛА, ЩО ОБЕРТАЄТЬСЯ. Зміст лекції. Теорема для повної кінетичної енергії тіла, що рухається поступово та обертальна. Перетворення Галілея. Механічний принцип відносності. Неінерціальні системи відліку. Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами т 1, т 2,..., тп, находящиеся на расстоянии r 1, r 2,.... rп от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
или
Используя эти выражения
где Jz – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
Из сравнения этой формулы с выражением для кинетической энергии тела, движущегося поступательно В случае плоского движения вращающегося тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m - масса катящегося тела; vC - скорость центра масс тела; JC - момент инерции тела относительно оси, проходящей через его центр масс; w - угловая скорость тела. Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):
M = Fr sina= Fl,
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис.26). Значение момента Мz не зависит от выбора положения точки О на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью
Найдем выражение для работы при вращении тела (рис.27). Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r,a- угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d j точка приложения В проходит путь ds = rd j, и работа равна произведению проекции силы на направление смещения на величину смещения:
Можем записать
где Fr sin a= Fl = Mz - момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но Учитывая, что Это уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r - радиус-вектор, проведенный из точки О в точку A; p = m v - импульс материальной точки (рис.28); L - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p. Модуль вектора момента импульса L = rp sin a= mvr sin a= pl, где a - угол между векторами r и р, l - плечо вектора р относительно точки О. Моментом импульса относительно неподвижной оси z называется скалярная величина L z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса L z не зависит от положения точки О на оси z. При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью v i. Скорость v i и импульс mi v i перпендикулярны этому радиусу, т.е. радиус является плечом вектора mi v i. Поэтому можем записать, что момент импульса отдельной частицы Liz = miviri и направлен по оси в сторону, определяемую правилом правого винта. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: Используя формулу vi =w ri , получим Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение по времени:
Это выражение - еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси : производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Имеет место векторное равенство Это выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. Закон сохранения момента импульса - фундаментальный закон природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
|

 .
.
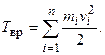

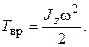
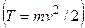 , следует, что момент инерции тела, участвующего во вращательном движении -есть мера инертности тела. Полученная формула справедлива для тела, вращающегося вокруг неподвижной оси.
, следует, что момент инерции тела, участвующего во вращательном движении -есть мера инертности тела. Полученная формула справедлива для тела, вращающегося вокруг неподвижной оси.

 Здесь М - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
Здесь М - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы где a - угол между r и F; r sina = l - кратчайшее расстояние между линией действия силы и точкой О - плечо силы.
где a - угол между r и F; r sina = l - кратчайшее расстояние между линией действия силы и точкой О - плечо силы.



 поэтому Mzd j= Jzwdw, или
поэтому Mzd j= Jzwdw, или 
 , получим
, получим 
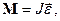 где J - главный момент инерции тела (момент инерции относительно главной оси).
где J - главный момент инерции тела (момент инерции относительно главной оси). Момент импульса и закон его сохранения При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы играет момент инерции. Аналогом импульса тела является момент импульса тела относительно оси.
Момент импульса и закон его сохранения При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы играет момент инерции. Аналогом импульса тела является момент импульса тела относительно оси.

 т.е. Lz = Jz w.
т.е. Lz = Jz w. т. е.
т. е.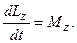
 В замкнутой системе момент внешних сил М =0 и
В замкнутой системе момент внешних сил М =0 и  , откуда L =const.
, откуда L =const.


