Гармонические колебания величины s описываются уравнением типа
где А - максимальное значение колеблющейся величины, называемое амплитудой колебаний, wo - круговая (циклическая) частота, j - начальная фаза колебаний в момент времени t =0, (wo t +j) - фаза колебаний и момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от + A до - A. Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2p, т. е. wo(t + T)+j = (wot+j)+2p, откуда T =2p/wo. Величина, обратная периоду колебаний, n=1/ T, т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая эти две формулы, получим wo=2pn. Единица частоты - герц (Гц):1 Гц - частота периодического процесса, при которой за 1 с совершается один цикл процесса. Запишем первую и вторую производные по времени от гармонически колеблющейся величины s (соответственно скорость и ускорение):
Из определения гармонических колебаний следует дифференциальное уравнение гармонических колебаний
(где учтено, что
Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью wо вокруг этой точки. Механические гармонические колебания. Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением:
Согласно выше изложенному скорость v и ускорение а колеблющейся точки соответственно равны
Сила F = ma, действующая на колеблющуюся материальную точку массой m, с учетом равна
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
|

 ,
,

 т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды скорости и ускорения соответственно равны
т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды скорости и ускорения соответственно равны 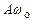 и
и  . Фаза скорости отличается от фазы смещения на p/2, а фаза ускорения отличается от фазы смещения на p. Следовательно, в моменты времени, когда s =0,
. Фаза скорости отличается от фазы смещения на p/2, а фаза ускорения отличается от фазы смещения на p. Следовательно, в моменты времени, когда s =0, 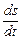 приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то
приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то  приобретает наибольшее положительное значение (рис.198).
приобретает наибольшее положительное значение (рис.198).
 Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис.199). Если этот вектор привести во вращение с угловой скоростью wо, то проекция конца вектора будет перемещаться по оси х и принимать значения от - А до + А, а колеблющаяся величина будет изменяться со временем по закону s= A cos(wo t +j).
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис.199). Если этот вектор привести во вращение с угловой скоростью wо, то проекция конца вектора будет перемещаться по оси х и принимать значения от - А до + А, а колеблющаяся величина будет изменяться со временем по закону s= A cos(wo t +j). .
.

 .
. ,
,


