Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна
Сложив формулы для кинетической и потенцвальной энергий, получим формулу для полной энергии:
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна. Из выведенных формул следует, что Т и П изменяются с частотой 2wо, т. е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 200 представлены графики зависимости х, Т и П от времени. Так как Гармонический осциллятор. Пружинный, физический и математический маятники Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида:
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур. 1. Пружинный маятник - это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = - kx, где k - коэффициент упругости, в случае пружины называемый жесткостью. Уравнение движения маятника
или
Отсюда следует, что пружинный маятник совершает гармонические колебания по закону
и периодом
Эти формулы справедливы для упругих колебаний в пределах, в которых выполняется закон Гука и когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, равна
Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы можно записать в виде
где J - момент инерции маятника относительно оси, проходящей через точку O, l - расстояние между точкой подвеса и центром масс маятника, Это уравнение можно записать в виде
или
Принимая получим уравнение
идентичное с уравнением для гармонического очциллятора, решение которого известно:
Следовательно, при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой wо и периодом
где L = J /(ml) - приведенная длина физического маятника. Точка О ' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника (рис.201). Применяя теорему Штейнера, получим
т. е. ОО ' всегда больше ОС. Точка подвеса О и центр качаний О ' обладают свойством взаимозаменяемости: если ось подвеса перенести в центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится. 3. Математический маятник - это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника J = ml 2, где l - длина маятника. Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке - центре масс, то, подставив момент инерции в формулу периода физического маятника, получим выражение для периода малых колебаний математического маятника
Сравнивая формулы пери ода для физического и математического маятников, видим, что если приведенная длина L физического маятника равна длине l математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Свободные затухающие колебания - колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах. Закон затухающих колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы - идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ. 1.Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде
Решение этого уравнения рассмотрим в виде
где и = u (f). После нахождения первой и второй производных выражения
Решение этого уравнения зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:
(если (
решением которого является функция Таким образом, решение искомого уравнения в случае малых затуханий (
где
Если A (t) и A (t+T)- амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм
- логарифмическим декрементом затухания; Ne - число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания Θ; - постоянная для данной колебательной системы величина. Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна
(так как затухание невелико ( Из формулы следует,что добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации. В заключение отметим, что при увеличении коэффициента затухания d период затухающих колебаний растет и при d=wo обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t Свободные затухающие колебания пружинного маятника. Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы F= - kx, сила трения пропорциональна скорости, т. е. где r - коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости. При данных условиях закон движения маятника будет иметь вид
Используя формулу
получим дифференциальное уравнение затухающих колебаний маятника:
Отсюда вытекает, что маятник колеблется по закону
с частотой РЕЗЮМЕ - При згасаючих коливаннях амплітуда коливань зменшується через втрати енергії в коливальній системі -Найпростішим механізмом зменшення енергії коливань є її перетворення в теплоту внаслідок тертя в механічних коливальних системах, а також омічних втрат і випромінювання електромагнітної енергії в електричних коливальних системах. - Якщо загасання мало, то можна умовно користуватися поняттям періоду як проміжку часу між двома наступними максимумами (або мінімумами) коливної фізичної величини -Проміжок часу, протягом якого амплітуда затухаючих коливань зменшується в е раз, називається часом релаксації. - Добротність коливальної сістеми пропорціональна числу коливань, що здійснюються системою за час релаксації. Контрольні питання - Що таке коливання? вільні коливання? гармонійні коливання? періодичні процеси? - Дайте визначення амплітуди, фази, періоду, частоти, циклічної частоти коливання. - Який зв'язок амплітуди і фази зміщення, швидкості і прискорення при прямолінійних гармонійних коливаннях? - В чому полягає ідея методу вектору амплітуди, що обертається? - Виведіть формули для швидкості і прискорення точки, що гармонійно коливається, як функції часу. - Виведіть і прокоментуйте формули для кінетичної, потенційної і повної енергії при гармонійних коливаннях. - Чому дорівнює відношення повної енергії гармонійного коливання до максимального значення повертаючої сили, що викликає це коливання? - Як можна порівняти між собою маси тіла, вимірюючи частоти коливань при підвішуванні цих мас до пружини? - Що називається гармонійним осцилятором? пружинним маятником? фізичним? математичним? - Що таке приведена довжина фізичного маятника? - Запишіть диференціальне рівняння затухаючих коливань і його рішення. Проаналізуйте їх для механічних і електромагнітних коливань. - Як змінюється частота власних коливань зі збільшенням маси тіла, що коливається? - За яким законом змінюється амплітуда затухаючих коливань? Чи є затухаючі коливання періодичними? - Чому частота затухаючих коливань має бути менше частоти власних коливань системи? - Що таке коефіцієнт загасання? декремент загасання? логарифмічний декремент загасання? У чому полягає фізичний сенс цих величин? -За якої умови відбувається аперіодичний процес? -За якої умови можна користуватися поняттям періоду у разі затухаючих коливань? ВИМУШЕНІ КОЛИВАННЯ. РІВНЯННЯ ХВИЛІ. Зміст лекції. Диференціальні рівняння вимушених коливань пружного маятника і заряду у коливальному контурі за умови дії відповідних змушуючих факторів. Їх розв'язок, вирази вимушених коливань. Резонанс. Хвильове рівняння. Біжуча хвиля. Рівняння хвилі, що розповсюджується у довільному напрямку. Різні форми рівняння. Вираз швидкості хвилі. Енергетичні характеристики хвилі. Вектор Умова. Рівняння стоячих хвиль. Теорія Максвела. Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Поставленную цель можно достичь двумя способами: 1.организовать автоколебательную систему, 2.использовать вынужденные колебания. Особенно важны и широко применимы так называемые автоколебания - незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой. Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний, происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями). Автоколебательная система состоит из четырех блоков: постоянно действующего источника энергии; колебательной системы; клапана, регулирующего количество энергии, поступающей от источника энергии в колебательную систему и обратной связи, посредством которой колебательная\ система сигназилирует клапану о необходимочсти поступления следующей порции энергии. Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй. Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т.д. При использовании вынужденных колебаний компенсация энергии возможна с помощью какого-либо периодически действующего фактора X (t), изменяющегося по гармоническому закону:
Если рассматривать механические колебания, то роль X (t) играет внешняя вынуждающая сила
С учетом вынуждающей силы закон движения для реального пружинного маятника запишется в виде
Используя описанный ранее ход рассуждений, придем к уравнению
Колебания, возникающие под действием внешней периодически изменяющейся силы называются вынужденными механическими колебаниями. Эти уравнения можно свести к линейному неоднородному дифференциальному уравнению
применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (х о в случае механических колебаний равно F o /m, в случае электромагнитных – U m /L). Решение линейного неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Частное решение неоднородного уравнения имеет вид
и частного решения, приведенного выше. Слагаемое
также зависят от w.
Упругие волны. Волновые процессы. Продольные и поперечные волны. Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами. Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества. Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных - в плоскостях, перпендикулярных направлению распространения волны.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис.220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением x частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Хотя приведенный график функции x (х, t) похож на график гармонического колебания, но они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний - зависимость смещения данной частицы от времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис.220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е. l =vT, или, учитывая, что Т= 1/n, где n - частота колебаний, v =ln. При переходе волны из одной среды в другую меняются ее длина волны и скорость, а частота не изменяется, так как она задается частотой источника колебаний (вибратором). Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т.е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени - один. Волновой фронт также является волновой поверхностью. В принципе волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение. Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н.А.Умова, решившего задачу о движении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.
На рис. 220 рассмотрим некоторую частицу среды В, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х =0, описываются функцией x(0, t)= А cosw t, то частица среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t, так как для прохождения волной расстояния х требуется время t= x/v, где v -скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид x(x, t)= A cos w(t - x / v), откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Данное уравнение есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то x(- x, t)= A cosw(t + x / v). В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид x(x, t)= A cos[w(t - x / v)+jo], где A =const - амплитуда волны,w - циклическая частота волны, jо - начальная фаза колебаний, определяемая в общем случае выбором начал отсчета х и t, [w(t - х / v) + jо] - фаза плоской волны. Для характеристики волн используется волновое число
Используя волновой вектор, уравнению бегущей волны можно придать вид ξ (x, t)= A cos(ω t - kx +φo). Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается только знаком члена kx. Предположим, что при волновом процессе фаза постоянна, т. е. ω(t - x / v)+ φo=const. Продифференцировав выражение и сократив на ω, получим
Следовательно, скорость v распространения волны в этом уравнении есть нечто иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.
|




 , то из формул следует, что
, то из формул следует, что  .
.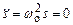 .
. ,
, .
. с циклической частотой
с циклической частотой
 .
. .
. 2. Физический маятник - это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела (рис.201).
2. Физический маятник - это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела (рис.201). ,
, - возвращающая сила (знак минус обусловлен тем, что направления Ft и a всегда противоположны;
- возвращающая сила (знак минус обусловлен тем, что направления Ft и a всегда противоположны;  соответствует малым колебаниям маятника, т. е. малым отклонениям маятника из положения равновесия).
соответствует малым колебаниям маятника, т. е. малым отклонениям маятника из положения равновесия). ,
, .
. ,
,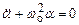 ,
, .
.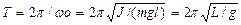 ,
, ,
, .
.
 где s - колеблющаяся величина, описывающая тот или иной физический процесс, δ=const - коэффициент затухания,ωo - циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
где s - колеблющаяся величина, описывающая тот или иной физический процесс, δ=const - коэффициент затухания,ωo - циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
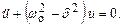

 )>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа
)>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа
 .
. )
)
 амплитуда затухающих колебаний, а A o- начальная амплитуда. Зависимость
амплитуда затухающих колебаний, а A o- начальная амплитуда. Зависимость  Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис.208). Тогда период затухающих колебаний равен
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис.208). Тогда период затухающих колебаний равен



 . Процесс не будет колебательным. Такой процесс называется апериодическим.
. Процесс не будет колебательным. Такой процесс называется апериодическим.



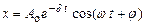
 (см. (146.4)). Добротность пружинного маятника,
(см. (146.4)). Добротность пружинного маятника, 
 .
. .
. .
.

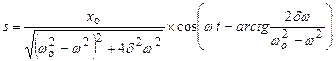
 Решение уравнения равно сумме общего решения однородного уравнения
Решение уравнения равно сумме общего решения однородного уравнения
 . Графически вынужденные колебания представлены на рис.209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями
. Графически вынужденные колебания представлены на рис.209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями
 Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т. е. фактически только в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах - как продольные, так и поперечные.
Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т. е. фактически только в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах - как продольные, так и поперечные. Для вывода уравнения бегущей волны - зависимости смещения колеблющейся частицы от координат и времени - рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис.220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от х и t, т. е. x=x(х, t).
Для вывода уравнения бегущей волны - зависимости смещения колеблющейся частицы от координат и времени - рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис.220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от х и t, т. е. x=x(х, t).
 , откуда
, откуда .
.


