Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения
При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул. По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой mо в газе, находящемся в состоянии равновесия при Т=const, остается постоянной и равной Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv,то на каждый интервал скорости будет приходиться некоторое число молекул dN(v),имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е.
Применяя методы теории вероятностей, Максвелл нашел функцию f(v) закон для распределения молекул идеального газа по скоростям:
Из формулы видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).
Относительное число молекул dN (v)/ N, скорости которых лежат в интервале от v до v+dv, находится как площадь более светлой полоски на рис.65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f (v)удовлетворяет условию нормировки
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав формулу Максвелла (постоянные множители опускаем) по аргументу v,приравняв результат нулю и используя условие для максимума выражения f (v): Значения v =0и
Из полученной формулы следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис.66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться. Средняя скорость молекулы
Подставляя сюда f (v)и интегрируя, получим
Скорости, характеризующие состояние газа: 1) наиболее вероятная Исходя из распределения молекул по скоростям
можно найти распределение молекул газа по значениям кинетической энергии Ɛ. Для этого перейдем от переменной v к переменной
где Таким образом, функция распределения молекул по энергиям теплового движения
Средняя кинетическая энергия
т.е. получили результат, совпадающий с ранее выведенными формулами. Барометрическая формула. Распределение Больцмана. При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.
где ρ - плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно, dp=- ρ gdh. Воспользовавшись уравнением состояния идеального газа pV= (m/M) RT (т - масса газа, М - молярная масса газа), находим, что
Подставив это выражение, получим
или
С изменением высоты от h 1до h 2 давление изменяется от р 1до р 2 (рис.67), т. е.
или
Это выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то формула может быть записано в виде
где р - давление на высоте h. Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром).Его работа основана на использовании барометрической формулы. Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ. Барометрическую формулу можно преобразовать, если воспользоваться выражением p = nkT:
где п - концентрация молекул на высоте h, п о- то же на высоте h = 0. Так как M=m o N A (N A - постоянная Авогадро, m о - масса одной молекулы), a R = kN A, то
где m o gh = П - потенциальная энергия молекулы в поле тяготения, т. е.
Полученной выражение называется распределением Больцмана во внешнем потенциальном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести. РЕЗЮМЕ - Процеси, які вивчаються молекулярною фізикою, є результатом сукупної дії величезного числа молекул -Як би не змінювалися швидкості молекул при зіткненнях, середня квадратична швидкість молекул масою mо в газі, що знаходиться в стані рівноваги при Т = const, залишається постійною. -Швидкість, при якій функція розподілу молекул ідеального газу за швидкостями максимальна, називається найбільш вірогідною швидкістю. - Барометрична формула дозволяє знайти атмосферний тиск залежно від висоти або, вимірявши тиск, знайти висоту. - Тиск з висотою убуває тим швидше, чим важче газ - З розподілу Больцмана у зовнішньому потенційному полі випливає, що при постійній температурі густина газу більше там, де менше потенційна енергія його молекул.
|

 . Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.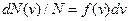 , откуда
, откуда .
.
 График функции f(v) приведен на рис.65. Так как при возрастании v множитель
График функции f(v) приведен на рис.65. Так как при возрастании v множитель  уменьшается быстрее, чем растет множитель v 2,то функция f (v), начинаясь от нуля, достигает максимума при ив и затем асимптотически стремится к нулю. Кривая несимметрична относительно v в.
уменьшается быстрее, чем растет множитель v 2,то функция f (v), начинаясь от нуля, достигает максимума при ив и затем асимптотически стремится к нулю. Кривая несимметрична относительно v в. .
. .
. соответствуют минимумам формулы, а значение v,при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v в:
соответствуют минимумам формулы, а значение v,при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v в: .
. (средняя арифметическая скорость) определяется по формуле
(средняя арифметическая скорость) определяется по формуле .
. .
. ;2) средняя
;2) средняя  ; З) средняя квадратичная
; З) средняя квадратичная  (рис.65).
(рис.65).
 . Подставив)
. Подставив)  в
в  , получим
, получим ,
, - число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от Ɛ до Ɛ + d Ɛ.
- число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от Ɛ до Ɛ + d Ɛ. .
. молекулы идеального газа
молекулы идеального газа ,
, Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р (рис.67), то на высоте h+dh оно равно р+dр (при dh >0 dp <0, так как давление с высотой убывает). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh соснованием площадью, равной единице площади:
Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р (рис.67), то на высоте h+dh оно равно р+dр (при dh >0 dp <0, так как давление с высотой убывает). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh соснованием площадью, равной единице площади: ,
, .
.
 .
. ,
, ,
, .
. ,
, ,
,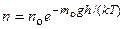 ,
, .
.


