ИНДУКТИВНОСТЬ КОНТУРА. САМОИНДУКЦИЯ.
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитое поле, индукция которого, по закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционалентоку I в контуре: F= LI, где коэффициент пропорциональности L называется индуктивностью контура. При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э. д.с. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн - индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/А = 1 В.с/А. Рассчитаем индуктивность бесконечно длинного соленоида. Полный магнитный поток через соленоид (потокосцепление) равен т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины /, площади S и магнитной проницаемости m, вещества, из которого изготовлен сердечник соленоида. Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура - аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции
Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L ==const и
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем возрастает, то
|
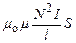. Подставив это выражение в формулу, получим 
,
.
,
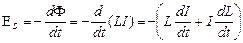и E s <0, т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возрастание. Если ток со временем убывает, то и E s <0, и E s >0,, т. е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.
