Пусть функция  определена в некоторой области
определена в некоторой области  .
.
Опр. Точка  , являющаяся внутренней точкой области определения функции
, являющаяся внутренней точкой области определения функции  , называется точкой максимума, если существует такое положительное число
, называется точкой максимума, если существует такое положительное число  , что для всех точек
, что для всех точек  выполняется неравенство
выполняется неравенство  .
.
Определение минимума дать самостоятельно.
Необходимое условие экстремума функции
Теорема Если точка  является точкой ext дифференцируемой в этой точке функции
является точкой ext дифференцируемой в этой точке функции  , то
, то  и
и  .
.
Опр. Точка, в которой частные производные равны 0, называется стационарной точкой функции.
Стационарные точки являются подозрительными на ext.
Геометрическая интерпретация необходимого условия ext
Пусть дана дифференцируемая функция  , точка
, точка  принадлежит области дифференцирования. Из условия, что
принадлежит области дифференцирования. Из условия, что  следует, что
следует, что
 и
и 
Проведем касательную плоскость к поверхности  в т.
в т.  .
.
 Ее уравнение 0 0
Ее уравнение 0 0

 Значит уравнение касательной плоскости
Значит уравнение касательной плоскости  - это горизонтальная плоскость (параллельна плоскости ХОУ).
- это горизонтальная плоскость (параллельна плоскости ХОУ).
В точке ext касательная плоскость горизонтальна.

Теорема (достаточное условие ext функции 2х переменных) Пусть функция  является дважды дифференцируемой в стационарной точке
является дважды дифференцируемой в стационарной точке  . Тогда если
. Тогда если
I. Определитель  , то стационарная точка
, то стационарная точка  является точкой ext, а именно: а) точкой max, если
является точкой ext, а именно: а) точкой max, если  и б) точкой min, если
и б) точкой min, если 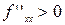 .
.
II. Если  , то стационарная точка
, то стационарная точка  не является точкой ext.
не является точкой ext.
III. В случае  ничего определенного сказать нельзя.
ничего определенного сказать нельзя.
Замечание: 
Пример.
Найти ext функции 
I шаг 
 ;
;
II шаг  или
или 
или 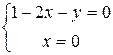 или
или  - стационарные точки.
- стационарные точки.
III шаг  ;
;  ;
; 
 ;
;
 ext нет
ext нет
 ext нет
ext нет
 ext нет
ext нет
 , ext есть.
, ext есть.  точка max
точка max  ,
,
а  .
.
Правило отыскания ext функции 


 определена в некоторой области
определена в некоторой области  .
. , являющаяся внутренней точкой области определения функции
, являющаяся внутренней точкой области определения функции  , что для всех точек
, что для всех точек  выполняется неравенство
выполняется неравенство  .
. и
и  .
. следует, что
следует, что
 Ее уравнение 0 0
Ее уравнение 0 0
 Значит уравнение касательной плоскости
Значит уравнение касательной плоскости  - это горизонтальная плоскость (параллельна плоскости ХОУ).
- это горизонтальная плоскость (параллельна плоскости ХОУ). является дважды дифференцируемой в стационарной точке
является дважды дифференцируемой в стационарной точке  , то стационарная точка
, то стационарная точка  и б) точкой min, если
и б) точкой min, если 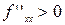 .
. , то стационарная точка
, то стационарная точка  ничего определенного сказать нельзя.
ничего определенного сказать нельзя.


 ;
; или
или 
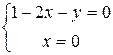 или
или  - стационарные точки.
- стационарные точки. ;
;  ;
; 
 ;
; ext нет
ext нет ext нет
ext нет ext нет
ext нет , ext есть.
, ext есть.  точка max
точка max  ,
, .
.



