Определение функции нескольких переменных
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
До сих пор мы изучали функции одной переменной y=f(x). На самом деле мир устроен сложнее, и не все можно описать с помощью функций одной переменной. Мы ограничимся изучением функций двух переменных, а затем распространим теорию на функции трех и более переменных Множества на плоскости Опр. Множество называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Опр. Множество называется ограниченным, если существует круг с центром в начале координат, целиком содержащий данное множество. (Можно рассматривать и прямоугольник, а не круг).
D1 – ограниченное множество D2 – нет D3 – нет Опр. Диаметром множества называется наибольшее расстояние между парами точек данного множества.
Точки А и В множества D находятся друг от друга на расстоянии d – оно самое наибольшее из всех расстояний между двумя любыми точками множества D.
Окрестность точки
Рассматривается и окрестность с выколотым центром.
Классификация точек по отношению к данному множеству
Опр. Точка М называется внутренней точкой множества, если она принадлежит множеству вместе с некоторой своей окрестностью. Опр. Точка М называется граничной точкой множества, если в любой ее окрестности есть как точки, принадлежащие множеству, так и точки ему не принадлежащие. Опр. Множество всех граничных точек данного множества образуют его границу. Замечание: граничные точки множества могут и не принадлежать точкам множества. Опр. Внешние точки это те, которые не являются ни внутренними, ни граничными. Опр. Не пустое множество, все точки которого внутренние, называется открытым. Опр. Не пустое множество, все граничные точки которого ему принадлежат, называется замкнутым. Опр. Областью называется открытое связное множество. Область вместе с границей образует замкнутую область. Определение функции 2х переменных Пусть дано два множества: R – множество действительных чисел и множество
Опр. Если каждому элементу множества Е по некоторому правилу или закону ставится в соответствие вполне определенный элемент из R, то говорят, что на множестве Е определена функция двух переменных х и y Множество Е – область определения функции Способы задания функции: аналитический, графический, табличный и др. Опр. Графиком функции двух переменных Как построить график функции На плоскости ХОУ изображается область определения Е. В каждой точке Но не так легко изображать поверхность на плоском листе. Поэтому для наглядности графика функции Опр. Множество всех точек плоскости, для которых функция имеет одинаковое значение, называется линией уровня. Уравнения линий уровня т.о. Пример: Построить линии уровня
и т.д.
Таким образом, поверхность Пример: Найти область определения функций: а) Решение: а)
б)
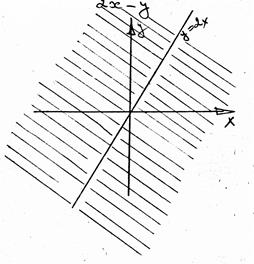
Ответ: все точки плоскости кроме точек, лежащих на прямой
|


 D1 – связное множество (односвязно) D2 – связное множество (многосвязно) нет
D1 – связное множество (односвязно) D2 – связное множество (многосвязно) нет

 ;
;  .
.
 - внешняя точка
- внешняя точка - внутренняя точка
- внутренняя точка - граничная точка
- граничная точка - множество упорядоченных пар действительных чисел.
- множество упорядоченных пар действительных чисел.
 , то есть графиком является поверхность в пространстве.
, то есть графиком является поверхность в пространстве. восстанавливаем перпендикуляр к плоскости ХОУ и откладываем на нем значение
восстанавливаем перпендикуляр к плоскости ХОУ и откладываем на нем значение  , где
, где  .
.
 - уравнения линий уровня
- уравнения линий уровня ,
,  - точка (0;0)
- точка (0;0) ,
, 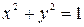 - окружность с центром в точке (0;0) и радиуса 1
- окружность с центром в точке (0;0) и радиуса 1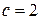 ,
, 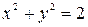 - окружность с центром в точке (0;0) и радиуса
- окружность с центром в точке (0;0) и радиуса 

 ; б)
; б) 



 или
или 

 или
или 
 Ответ: все точки плоскости, лежащие в вертикальных углах, образующихся прямыми
Ответ: все точки плоскости, лежащие в вертикальных углах, образующихся прямыми  и
и  .
.

 .
.


