Опр. Число  называется пределом функции
называется пределом функции  в точке
в точке  , если для любого
, если для любого  , найдется такое
, найдется такое  , что из условия: точка
, что из условия: точка  является точкой
является точкой  -окрестности т.
-окрестности т.  с выколотым центром вытекает выполнение неравенства
с выколотым центром вытекает выполнение неравенства
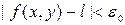



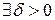



Из определения, очевидно, что если предел функции в точке существует, то он не зависит от пути следования т.  к т.
к т.  .
.
Пример 1:
 .
. 
Показать, что функция не имеет предела в т.  .
.
Решение:
Область определения функции – все точки плоскости ХОУ, кроме т.  .
.
Для того чтобы убедиться, что в т.  функция не имеет предел, достаточно заметить, что при приближении переменной точки
функция не имеет предел, достаточно заметить, что при приближении переменной точки  к т.
к т.  вдоль биссектрисы 1-го координатного угла
вдоль биссектрисы 1-го координатного угла  значение функции
значение функции  все время остается неизменным и равным 0.
все время остается неизменным и равным 0.
Если же приближаться к т.  вдоль каких-либо других линий, то значения функции будут приближаться к другим числам. Так, например, если двигаться вдоль положительной полуоси ОУ
вдоль каких-либо других линий, то значения функции будут приближаться к другим числам. Так, например, если двигаться вдоль положительной полуоси ОУ  , то значение функции остается все время равным -1 (то есть во всех точках этой полуоси
, то значение функции остается все время равным -1 (то есть во всех точках этой полуоси  ).
).
Таким образом, при приближении к точке  по различным путям функция стремится к различным значениям. Следовательно, функция не имеет предела при
по различным путям функция стремится к различным значениям. Следовательно, функция не имеет предела при 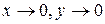 .
.
Аналогично тому, как это делалось для функции одной переменной, можно доказать, что и для функций двух переменных предел суммы двух функций равен сумме их пределов; предел произведения равен произведению пределов сомножителей; предел частного равен частному от деления предела числителя на предел знаменателя (при условии, что предел делителя отличен от нуля).
Отметим также, что разность между функцией, имеющей предел, и ее пределом есть, очевидно, бесконечно малая функция. (функция  называется бесконечно малой в точке, если ее предел в этой точке равен 0).
называется бесконечно малой в точке, если ее предел в этой точке равен 0).
Опр.1 Функция  называется непрерывной во внутренней точке
называется непрерывной во внутренней точке 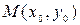 области Е, где определена функция, если
области Е, где определена функция, если  .
.
Если учесть, что  ,
,  ,
,  , то определение 1 перейдет в
, то определение 1 перейдет в
Опр. 2 Функция непрерывна в точке  , если приращение функции
, если приращение функции  стремится к нулю, при стремлении к нулю приращений
стремится к нулю, при стремлении к нулю приращений  и
и  , то есть
, то есть  .
.
Опр. Функция  называется непрерывной в области, если она непрерывна в каждой точке области.
называется непрерывной в области, если она непрерывна в каждой точке области.
Свойства непрерывных функций
Функции, непрерывные во всех точках некоторой замкнутой ограниченной области, обладают следующими свойствами, которые приведем без доказательств.
Т 1 (об ограниченности функции) Функция  , непрерывная в замкнутой, ограниченной области, ограничена в этой области
, непрерывная в замкнутой, ограниченной области, ограничена в этой области  , т.е.
, т.е.  ,
,  .
.
Т 2 (о наибольшем и наименьшем значениях функции) Непрерывная в замкнутой, ограниченной области  функция
функция  принимает в этой области наибольшее и наименьшее значения.
принимает в этой области наибольшее и наименьшее значения.
Это означает, что в данной области  существуют точки
существуют точки  и
и  , что для всех точек
, что для всех точек  имеет место неравенства
имеет место неравенства
 и
и 
Говорят, что в точке  функция
функция  достигает наибольшего значения в данной области, а в точке
достигает наибольшего значения в данной области, а в точке  - наименьшего.
- наименьшего.
Замечание: Если рассматривать функцию непрерывную не в замкнутой и ограниченной области, то Т 1 и Т2 могут оказаться неверными.
Т 3 (о промежуточных значениях) Пусть функция  непрерывна в некоторой области
непрерывна в некоторой области  . Тогда каковы бы ни были точки
. Тогда каковы бы ни были точки  и
и  этой области, для любого числа с, заключенного между
этой области, для любого числа с, заключенного между  и
и  , существует в области
, существует в области  такая точка
такая точка  , что
, что  .
.
В частности, если  , а
, а 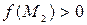 , то в области
, то в области  найдется такая точка, в которой значение функции равно нулю.
найдется такая точка, в которой значение функции равно нулю.

 называется пределом функции
называется пределом функции  в точке
в точке  , если для любого
, если для любого  , найдется такое
, найдется такое  , что из условия: точка
, что из условия: точка  является точкой
является точкой  -окрестности т.
-окрестности т. 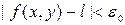



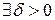



 .
. 
 .
. к т.
к т.  вдоль биссектрисы 1-го координатного угла
вдоль биссектрисы 1-го координатного угла  значение функции
значение функции  , то значение функции остается все время равным -1 (то есть во всех точках этой полуоси
, то значение функции остается все время равным -1 (то есть во всех точках этой полуоси  ).
).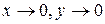 .
. называется бесконечно малой в точке, если ее предел в этой точке равен 0).
называется бесконечно малой в точке, если ее предел в этой точке равен 0).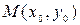 области Е, где определена функция, если
области Е, где определена функция, если  .
. ,
,  ,
,  , то определение 1 перейдет в
, то определение 1 перейдет в , если приращение функции
, если приращение функции  стремится к нулю, при стремлении к нулю приращений
стремится к нулю, при стремлении к нулю приращений  и
и  , то есть
, то есть  .
. называется непрерывной в области, если она непрерывна в каждой точке области.
называется непрерывной в области, если она непрерывна в каждой точке области. , т.е.
, т.е.  ,
,  .
. и
и  , что для всех точек
, что для всех точек  имеет место неравенства
имеет место неравенства и
и 
 непрерывна в некоторой области
непрерывна в некоторой области  и
и  этой области, для любого числа с, заключенного между
этой области, для любого числа с, заключенного между  и
и  , существует в области
, существует в области  .
. , а
, а 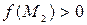 , то в области
, то в области 


