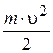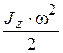Момент импульса и закон его сохранения
Моментом импульса (количеством движения) материальной точки A относительно неподвижной точки O называется физическая величина, определяемая векторным произведением:
где r – радиус-вектор, проведённый из точки O в точку A;
L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p.
Модуль вектора момента импульса:
где a – угол между векторами r и p, l – плечо вектора p относительно точки O. Моментом импульса материальной точки A относительно неподвижной оси Z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса. Значение момента импульса Lz не зависит от положения точки O на оси Z. Моментом импульса материальной точки:
и направлен по оси в сторону, определяемую правилом правого винта. Момент импульса твердого тела относительно оси есть сумма моментов импульсов отдельных материальных точек:
Используя формулу
таким образом:
где Jz – момент инерции тела; w – угловая скорость. Продифференцировав последнее уравнение по времени, получим:
т.е. Это выражение - ещё одна форма уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси. В замкнутой системе момент внешних сил M =0 и
Выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не меняется с течением времени.
Основная связь между величинами и уравнениями, определяющие вращение тела вокруг неподвижной оси и его поступательном движении:
|

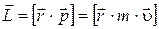
 – импульс материальной точки (рис. 4.1.);
– импульс материальной точки (рис. 4.1.);



 , получим:
, получим:


 .
.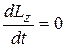 , откуда:
, откуда: .
.