Ускорение и его составляющие
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Средним ускорением неравномерного движения в интервале от t до t + D t называется векторная величина, равная отношению изменения скорости Du к интервалу времени D t:
Мгновенным ускорением a материальной точки в момент времени t будет предел среднего ускорения:
Таким образом, ускорение a есть векторная величина, равная первой производной скорости по времени. Тангенциальная составляющая ускорения:
т. е., равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Вторая составляющая ускорения:
В пределе при t + D t получим u1 ® u.
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру её кривизны (поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 3.2.):
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом: 1) at =0, an =0 — прямолинейное равномерное движение; 2) at = a = const, an = 0 — прямолинейное равнопеременное движение. При таком виде движения:
Если начальный момент времени t1 = 0, а начальная скорость u1 = uo, то обозначив t2 = t и u2 = u, получим
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдём, что длина пути, пройденного точкой, в случае равнопеременного:
3) at = f(t), an = 0 — прямолинейное движение с переменным ускорением; 4) at = 0, an = const. При at = 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы an=u2/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным; 5) at =0, an ¹; 0 — равномерное криволинейное движение; 6) at = const, an¹ 0 — криволинейное равнопеременное движение; 7) at =f(t), an¹; 0 — криволинейное движение с переменным ускорением.
|


 (3.1)
(3.1)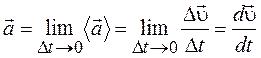


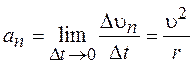


 .
. , откуда:
, откуда: .
.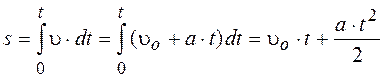 ;
;


