Потенциальная энергия может быть определена исходя из (2.3) как
где C – постоянная интегрирования. Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести
где
Эта работа равна изменению некоторой физической величины Ep = mgh. Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком. A = –(Ep2 – Ep1). Найдём потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:
где F упр — проекция силы упругости на ось х, k — коэффициент упругости (для пружины – жёсткость), знак минус указывает, что Fупр направлена в сторону, противоположную деформации х. По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.
Элементарная работа dA, совершаемая силой Fx при бесконечно малой деформации dx, равна:
а полная работа
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела:
Полная механическая энергия системы:
т.е. равна сумме кинетической и потенциальной энергий. § 3. Закон сохранения энергии
Рассмотрим систему материальных точек массами т 1, т 2..., т n и движущихся со скоростями u1, u2..., un. Пусть F' 1, F' 2,..., F'n — равнодействующие внутренних консервативны сил, F 1, F 2..., Fn — равнодействующие внешних сил, а f 1, f 2..., fn — равнодействующие внешних консервативных сил. Второй закон Ньютона для каждого из n тел механической системы:
………………
Умножим каждое из уравнений на соответствующее перемещение и, учитывая, что
………………
Сложив эти уравнения, получим:
где dЕк – кинетическая энергия системы. Второй член Правая часть равенства (3.1) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем
При переходе системы из состояния 1 в какое-либо состояние 2:
т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.2) следует, что:
откуда
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (3.3) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Рис. 3.1 поясняет решение этой задачи.
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
Из этих соотношений следует:
Центростремительное ускорение в нижней точке создается силами
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно:
Прочность нити должна, очевидно, превышать это значение.
|

 (2.4)
(2.4) . Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения
. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения  на ось OY:
на ось OY:
 – проекция силы тяжести, ΔS y – проекция вектора перемещения. Если тело переместилось из точки, расположенной на высоте h 1, в точку, расположенную на высоте h 2 от начала координатной оси OY(рис. 2.2.), то сила тяжести совершила работу:
– проекция силы тяжести, ΔS y – проекция вектора перемещения. Если тело переместилось из точки, расположенной на высоте h 1, в точку, расположенную на высоте h 2 от начала координатной оси OY(рис. 2.2.), то сила тяжести совершила работу: .
.
 , взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести


 .
.

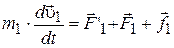 ,
,  ,
, ,
, , получим:
, получим: ,
,  ,
, ,
, (3.1)
(3.1) .
. равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dEпот системы.
равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dEпот системы. (3.2)
(3.2)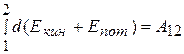
 ,
,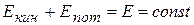 ,(3.3)
,(3.3)

 натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.

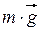 направленными в противоположные стороны:
направленными в противоположные стороны: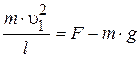
 .
.


